 В этом году фактически было присуждено две Нобелевских премии по физике: одна — Джорджо Паризи (Giorgio Parisi) за работы в области конденсированных сред, другая — Сюкуро Манабе (Syukuro Manabe) и Клаусу Хассельману (Klaus Hasselmann) за исследования в области климатологии. Эти премии не имеют между собой ничего общего, хотя их попытались объединить формулировкой «сложные системы». К сожалению, дележ Нобелевской премии на две (пока еще не на три) не связанные части становится традицией: например, в 2019 году одну часть дали за открытие экзопланет, вторую — за космологию, это вообще разные науки. Вероятно, такой дележ — следствие каких-то компромиссов, но престижа премии это не добавляет. Так или иначе, про премию по физике этого года приходится публиковать две разные статьи разных авторов.
В этом году фактически было присуждено две Нобелевских премии по физике: одна — Джорджо Паризи (Giorgio Parisi) за работы в области конденсированных сред, другая — Сюкуро Манабе (Syukuro Manabe) и Клаусу Хассельману (Klaus Hasselmann) за исследования в области климатологии. Эти премии не имеют между собой ничего общего, хотя их попытались объединить формулировкой «сложные системы». К сожалению, дележ Нобелевской премии на две (пока еще не на три) не связанные части становится традицией: например, в 2019 году одну часть дали за открытие экзопланет, вторую — за космологию, это вообще разные науки. Вероятно, такой дележ — следствие каких-то компромиссов, но престижа премии это не добавляет. Так или иначе, про премию по физике этого года приходится публиковать две разные статьи разных авторов.
Борис Штерн


Формулировка Нобелевской премии по физике 2021 года замечательна по своей бессодержательности: «for groundbreaking contributions to our understanding of complex systems». Понятное дело, все «простые» системы уже давно исследованы и соответствующие премии давно получены. Словосочетание «исследования сложных систем» давно стало признаком пустой болтовни вместо реальной науки. Не менее бессмысленна и формулировка конкретного достижения Джорджо Паризи, получившего ½ премии: «for the discovery of the interplay of disorder and fluctuations in physical systems from atomic to planetary scales» («за открытие взаимодействия неупорядоченностей и флуктуаций в физических системах от атомарного до планетарного масштабов»). Паризи не занимался ни атомами, ни планетами. Однако ему действительно принадлежит очень важное достижение в теоретической физике — он сделал первый значительный шаг в создании теории спиновых стекол и других неэргодических систем. О сути этого достижения и стоит рассказать. Заодно станет понятно, что никакой связи между теорией Паризи и работами двух других лауреатов 2021 года — специалистов по климату Сюкуро Манабе и Клауса Хассельмана — не существует. С тем же успехом можно было бы объединять Паризи со специалистами по физике высоких энергий или по физике плазмы.
Disclaimer: я понятия не имею, по каким именно причинам члены Нобелевского комитета присудили Паризи эту премию. Я могу только рассказать, что по поводу его научных заслуг думают профессионалы, сами работавшие в этой области (причем и среди них возможны разные мнения).

Начать необходимо с предыстории. К середине 1970-х годов появились внятные экспериментальные данные о существовании фазового перехода необычного типа в разбавленных магнитных сплавах, где магнитными атомами являются марганец (Mn) или железо (Fe), и их доля очень мала, в то время как «матрица» из меди (Cu) или золота (Au) — простой немагнитный металл. Чтобы объяснить, чем замечательны эти сплавы, придется сначала обратиться к еще более старому и классическому вопросу об обычном магнетизме металлов. В чистом железе магнитные моменты атомов упорядочиваются при температуре ниже «точки Кюри» (Tc = 1043 K) вдоль одного общего направления — такое состояние называется ферромагнитным. В чистом марганце тоже возникает упорядочение, но другое — антиферромагнитное: магнитные моменты чередуют свои направления — «вверх» и «вниз» относительно некоторой общей оси, и такое состояние возникает при температуре ниже «точки Нееля» TN = 100 K. Появление таких упорядоченных состояний обусловлено видом взаимодействия между магнитными моментами: для железа энергия взаимодействия двух моментов минимальна, когда их направления параллельны, в то время как для марганца минимум энергии отвечает антипараллельной ориентации магнитных моментов.
В разбавленных твердых сплавах марганца в меди или железа в золоте (и во многих других подобных) взаимодействие между различными магнитными моментами знакопеременно — одни пары моментов предпочитают параллельную ориентацию, а другие — антипараллельную. В результате конкуренции этих взаимодействий магнитные моменты оказываются направлены хаотически — кто куда. При этом, что важно, было обнаружено существование некоторой характерной температуры Tg (своей для каждого сплава), при которой с системой «что-то происходит» — т. е. наблюдается аномалия в зависимостях термодинамических величин от температуры. При охлаждении ниже Tg качественно меняется динамика магнитных моментов. При T ниже Tg каждый отдельный магнитный момент Si приобретает среднее направление <Si> = mi , в то время как при T выше Tg все величины mi = 0, потому что текущие направления магнитных моментов Si быстро меняются во времени. На языке статистической механики фазовый переход, происходящий при понижении температуры ниже Tg, называется «нарушением эргодичности». Яркий пример не-эргодичности — зависимость состояния системы не только от внешних параметров (как температура T или магнитное поле H), но и от того пути, по которому систему привели в заданную точку на плоскости (H, T). Именно это и наблюдается в таком магнитном сплаве: если вначале включить магнитное поле H и затем охладить его до T ниже Tg то появится намагниченность M1(H, T); если же сначала охладить до той же температуры T, а потом включить такое же поле H, то появится намагниченность M2(H, T) заметно меньшая, чем M1(H, T). Отличие M1 от M2 имеет место только для температур T, меньших, чем Tg, — именно в этом смысле Tg и есть температура нарушения эргодичности.
К середине 1970-х годов стало понятно: нарушение эргодичности в таких магнитных сплавах представляет собой фазовый переход — т. е. состояния вещества выше и ниже точки перехода качественно различны. Но описать этот переход при помощи классической теории, созданной Л. Д. Ландау еще в 1930-х, не удавалось: было непонятно, что в таком фазовом переходе следует понимать под «параметром порядка» — той величиной, которая качественно отличает упорядоченную фазу от неупорядоченной.
Важный шаг был сделан в 1975 году в работе С. Эдвардса (S. Edwards) и П. У. Андерсона (P. W. Anderson) «Theory of spin glasses». Они предложили использовать в качестве параметра порядка средний по системе квадрат локальной намагниченности q = (1/N) Σi mi2 и решили называть такие магнитные состояния «спиновым стеклом» — по аналогии с обычным стеклом, которое похоже на кристалл своей «твердостью», но отличается от него тем, что атомы в нем расположены хаотично. Вскоре Д. Шеррингтон (D. Sherrington) и С. Киркпатрик (S. Kirkpatrick) представили (казалось бы точное) решение упрощенной версии модели Эдвардса и Андерсона, считая параметром порядка величину q.
И тут выяснилось нечто крайне странное: это решение приводило к бессмысленному утверждению об отрицательности энтропии системы при низких температурах. Но энтропия отрицательной не бывает — значит, с «точным решением» что-то было не в порядке. Тут надо заметить, что с математической точки зрения теории Эдвардса — Андерсона и Шеррингтона — Киркпатрика содержали в качестве параметра порядка не просто число q, но некоторую квадратную n×n матрицу qαβ, причем число n вначале считалось целым, а в конце вычислений его надо было устремить к нулю. Значки α и β, пробегавшие значения от 1 до n, называют «репличными индексами», потому что это теоретическое описание технически подразумевало работу с n «репликами» исходной физической системы. При этом все считали, что недиагональные (α ≠ β) элементы этой матрицы равны между собой и совпадают с параметром порядка q, введенным Эдвардсом и Андерсоном (а все элементы qαα = 0 по тривиальной причине). Не видно было никаких причин ожидать различия между элементами qαβ с разными парами индексов α и β.
Вот здесь на сцену и выходит Паризи: в 1979–1981 годах им была опубликована серия статей, предлагавших совершенно неожиданный выход из «тупика отрицательной энтропии».
Паризи понял, что в состоянии спинового стекла матрица qαβ теряет свою — казалось бы, очевидную — симметрию, и предложил неожиданный и очень красивый способ описать, как именно эта симметрия нарушается. Проиллюстрировать его идею проще на рисунках:
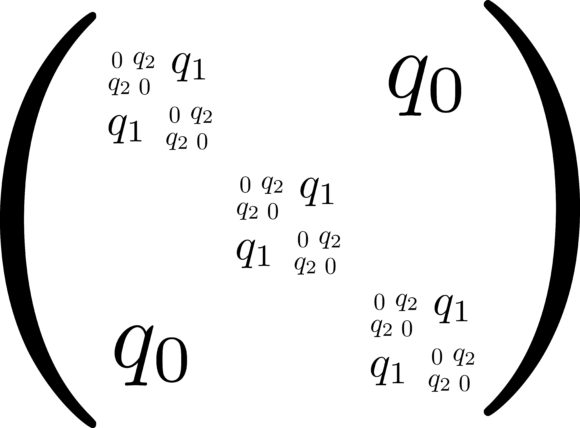
Рис. 1а показывает «наивную» симметричную матрицу n×n, которая задается лишь одним числом q0. На рис. 1б появляется два нетривиальных числа вне диагонали — q0 и q1. При этом появляется еще один параметр — размер m блоков, на которые разбивается вся n×n матрица (число таких блоков n/m). Это простейший пример нарушения «репличной симметрии» — на один шаг. Ближе к диагонали стоят числа q1 а подальше от нее — q0. На рис. 1в показана наша матрица после 2-го шага, теперь она характеризуется числами q0, q1 и q2 а также размерами m1 и m2 внешнего и внутреннего матричных блоков. Продолжение схемы на следующие шаги нарушения симметрии теперь вполне очевидно, в конечном счете оно приводит к описанию состояния системы при помощи непрерывной и монотонной функции q(x), определенной для интервала значений x между 0 и 1. Эта функция подчиняется интегро-дифференциальному уравнению, которое можно решить численно, а в некоторых случаях и аналитически.
Конструкция Паризи выглядела поначалу совершенно абстрактной и формальной, но она решала «парадокс отрицательной энтропии»: решение Паризи с нарушенной репличной симметрией приводит к энтропии S(T), стремящейся к нулю при T→0, как это и должно быть в соответствии с общими представлениями статистической физики. Стало ясно, что это действительно крупный прорыв в создании теории стекол.
Дальше стало выясняться, что предложенная схема Паризи имеет очень интересный и глубокий физический смысл. Как мы видим на рис. 1, нарушение репличной симметрии устроено иерархическим (или древесным) образом: сначала возникает различие между элементами матрицы qab, находящимися вдали от главной диагонали (q0) и вблизи от нее (q1); однако понятие «вблизи диагонали» можно понимать по-разному, и на втором шаге появляется уже три разных значения элементов qab — самые близкие к диагонали элементы q2 отличаются от несколько более удаленных q1 (а наиболее удаленные от диагонали q0 уже не меняются, их значения такие же, как на первом шаге)1.
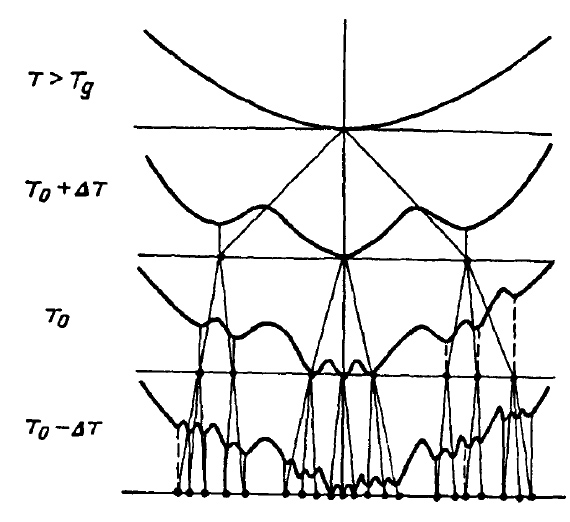
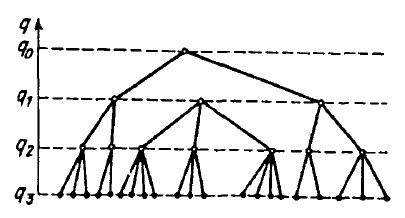
Удивительно, но оказалось возможным показать, что эта формальная иерархия в построении матриц qαβ — она продемонстрирована на рис. 2а — имеет свою аналогию в устройстве физических состояний, реализующих локальные минимумы энергии спинового стекла — рис. 2б. Выше шла речь о том, что состояние стекла при T ниже Tg неэргодично и зависит от «истории системы» — от того, по какому пути мы пришли в точку с заданной температурой и магнитным полем. Так происходит именно потому, что стекло имеет множество различных «локально устойчивых» конфигураций магнитных моментов.
В mi(a) верхний индекс (a) как раз и обозначает номер такой конфигурации. Перейти из одного локально устойчивого состояния (a) в другое (b) трудно — это требует преодоления большого энергетического барьера, а значит, и очень большого времени. Один из совершенно нетривиальных выводов теории Паризи состоит в том, что эти различные состояния образуют своеобразную древесную (или иерархическую) структуру, именно она схематически изображена на рис. 2б2.
С физической точки зрения иерархичность пространства метастабильных состояний демонстрирует, что новые метастабильные состояния mi(a) — «потомки» — появляются по мере понижения температуры путем ветвления уже имевшихся (при более высокой температуре) состояний — «предков». Именно это и изображено на рис. 2б.
Таким образом, формальная (и поначалу не очень математически строгая) теория привела к фундаментальной картине устройства спиновых стекол — и множества других подобных систем, о чем ниже.
В действительности значение схемы Паризи выходит далеко за пределы теории магнитных сплавов, с которых всё это начиналось. Для появления «стекольности» в поведении сильно взаимодействующей системы при низких температурах достаточно двух довольно распространенных свойств:
1) Взаимодействия должны быть «взаимно конкурирующими» — т. е. разные части энергии взаимодействия навязывают системе различные типа упорядочения (это свойство часто называется «фрастрацией»).
2) В параметрах взаимодействия системы должен присутствовать изначально заложенный беспорядок (в случае наших магнитных сплавов — это случайные положения магнитных атомов в немагнитной матрице). Таких физических систем великое множество, они могут состоять из магнитных моментов или электрических диполей, а могут быть и сверхпроводящими (например, ранние образцы высокотемпературных сверхпроводников, помещенные в магнитное поле, демонстрировали «стекольные» свойства). Более того, свойство (2) даже не является вполне обязательным: ведь существуют и стекла в самом обычном смысле — «оконные» — аморфное твердое тело, состоящее преимущественно из двуокиси кремния. Это вещество может существовать в виде кристаллов (кварц различных модификаций), которые вырастают при медленном охлаждении расплава. Если же охлаждать расплав быстро, кристаллическое состояние не успевает сформироваться, а вместо него возникает состояние стекольного характера. Таким же образом ведут себя многочисленные другие вещества, образующие стекольные фазы вместо кристаллических. К этим случаям также применима некоторая модификация развитой Паризи теории «нарушения репличной симметрии».
Всё сказанное выше не означает, что открытие Паризи исчерпывает проблему создания теории спиновых и других стекол. На самом деле эта теория непосредственно применима лишь к сильно упрощенной модели стекла, которая не учитывает конечность радиуса взаимодействия составляющих стекло элементов (магнитных моментов и т. п.). Дискуссия о том, в какой степени такая теория соответствует реальным физическим системам в трехмерном пространстве, длится уже 40 лет, и не все согласятся, что этот вопрос окончательно решен. Мое мнение таково: главные черты реального стекла теория Паризи ухватывает правильно, но есть много «подробностей», в том числе и весьма важных, которые пока никто описать теоретически не умеет.
Весьма важно, что применения теории Паризи выходят далеко за пределы собственно физических объектов. Существует по меньшей мере две крупные области computer science, к которым прямо относятся результаты теории Паризи. Это задачи о создании систем распределенной памяти (или «нейронные сети») и задачи нелинейной оптимизации по очень большому числу параметров. Осознание глубоких аналогий между теорией стекол и этими проблемами возникло довольно рано, уже в середине 1980-х годов, и привело к массе интересных результатов. У меня нет сомнений, что со временем будут развиты приложения этой теории и к проблемам, казалось бы, совсем далеким от физики и математики, — ибо проблематика «конкуренции» и «беспорядка» является крайне широко распространенной в разнообразных сферах человеческой деятельности.
В заключение замечу, что Джорджо Паризи имеет ряд крупных достижений и в других направлениях теоретической физики. Но это уже другая история, и ее может описать кто-то еще.
Михаил Фейгельман,
гл. науч. сотр. ИТФ им. Л. Д. Ландау,
зав. базовой кафедрой МФТИ «Проблемы теоретической физики»
1 Подобную ситуацию описал Фазиль Искандер в книге «Кролики и удавы» (1982). Там фигурировали просто кролики (в наших обозначениях это q0), были кролики, допущенные к столу короля (q2), а также кролики, еще пока только стремящиеся быть допущенными к столу короля (q1).
2 Картинки, использованные для рис. 2, взяты из обзора Доценко В. С. «Физика спиновых стекол» // Успехи физических наук, 163, 1 (1993), который я искренне рекомендую для всех, кто хочет углубиться в вышеизложенную тему.
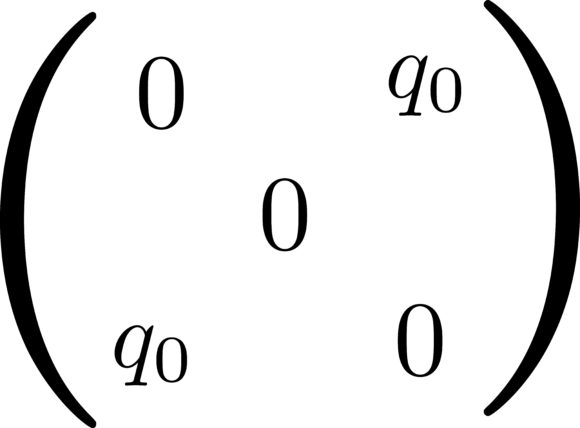
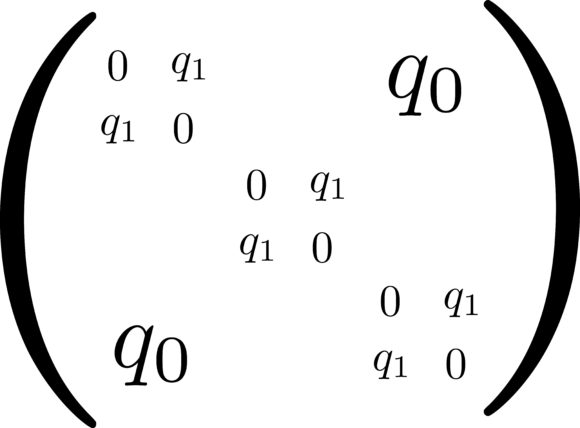

 (6 оценок, среднее: 4,17 из 5)
(6 оценок, среднее: 4,17 из 5)
В аспирантские годы (80-е) я потратил уйму времени, чтобы понять, что сделал Паризи. Так и не понял ничего. Вот совсем-совсем не понял. А эта популярная статья довольно хорошо все объяснила. Прямо «глаза открылись».