Эти загадочные энионы

В последние годы физики и инженеры всё чаще обсуждают перспективы практического применения экзотических квазичастиц, которые могут существовать только в двумерных или одномерных квантовых системах при сверхнизких температурах. Хотя пока что эти перспективы выглядят неблизкими, вера в их конечную реальность уже находит немало сторонников. В то же время даже название частиц, приведенное в заголовке статьи, пока не слишком известно широкой публике, а те идеи и концепции, которые за ним стоят, — тем более. Думаю, что в год столетия квантовой механики рассказ о них будет весьма уместным.

Откуда есть пошли энионы

Странное слово из заголовка проникло в язык теоретической физики 43 года назад. Оно было придумано для обозначения гипотетических квантовомеханических объектов, занимающих промежуточное положение между бозонами и фермионами. В 1982 году американский физик-теоретик и будущий нобелевский лауреат Фрэнк Вилчек предположил, что такими объектами могут быть заряженные частицы, обращающиеся вокруг трубок магнитных силовых линий¹. Это была чисто умозрительная конструкция, которой в то время нельзя было приписать никакой физической реальности, подтвержденной экспериментом. Как отметил сам Вилчек во второй из упомянутых статей, «практические применения рассмотренных феноменов выглядят весьма отдаленными», однако их теоретический анализ «представляет несомненный методологический интерес и позволяет увидеть в новом свете фундаментальные связи между спином и статистикой». Эту мысль он повторил и в конце статьи: «Исследование того, как статистическая механика большого числа свободных энионов интерполирует между бозонами и фермионами, представляет собой весьма интригующую математическую проблему».

Поскольку экзотические структуры Вилчека всё же нуждались в имени, он окрестил их «энионами» (anyons). Это слово он образовал как комбинацию местоимения any (всякий, любой) и традиционного окончания названий элементарных частиц на —on (proton, electron, neutron). Тем самым он подчеркнул, что взаимные парные перестановки энионов могут менять фазу описывающей их волновой функции любым образом, а не только двумя способами, один из которых соответствует бозонам, а другой — фермионам (подробнее об этом чуть ниже). Конечно, вилчековский неологизм не имеет ничего общего со всем известными анионами (anions), отрицательно заряженными ионами в электролитах.

Кое-что о квантовых статистиках

Чтобы прояснить только что сказанное, имеет смысл напомнить, что такое бозоны и фермионы. Рассмотрим систему одинаковых квантовых частиц — скажем, электронное облако вокруг атомного ядра. Каждая находится в каком-то из разрешенных ей квантовых состояний, набор которых дискретен.

Количество частиц, одновременно пребывающих в одном и том же состоянии, называется числом заполнения. Еще в 1920-е годы физики пришли к выводу, что микрочастицы подразделяются на два непересекающихся класса. Числа заполнения частиц одной группы в принципе могут принимать любые целочисленные значения: 0 (состояние пусто), 1, 2, 3, 4 и т. д. вплоть до бесконечности. Частицы другого типа в коллективе ведут себя совершенно иначе, их числа заполнения — или нуль, или единица. Таким образом, в каждом разрешенном состоянии может сидеть не больше одной такой частицы, а две — это уже слишком много. Частицы первого типа подчиняются квантовой статистике Бозе — Эйнштейна и называются бозонами. Частицы второй группы проходят по ведомству статистики Ферми — Дирака и именуются фермионами.

Долгое время считалось, что никаких других частиц, кроме бозонов и фермионов, просто не существует. Эта уверенность распространялась и на квазичастицы, возбужденные состояния многочастичных систем (их также называют коллективными возбуждениями), в ряде отношений проявляющие себя как «настоящие» частицы. К примеру, это электроны проводимости и дырки в полупроводниках, а также фононы — квантованные низкотемпературные колебания кристаллической решетки.

Во многих учебниках математически доказывается, что общие принципы квантовой механики не допускают существования никаких иных частиц, кроме бозонов и фермионов. Схема таких доказательств довольно проста. Возьмем квантовую систему из любого числа одинаковых частиц, которая, как ей и положено, описывается волновой функцией, зависящей, для простоты, только от координат каждой частицы. Если мы поменяем местами любую пару частиц, а потом совершим этот обмен вторично, система окажется в исходном состоянии. Согласно принципам квантовой механики, это означает, что при любой парной перестановке частиц волновая функция всей системы подвергается действию преобразования, которое при повторном применении возвращает ее к прежнему значению. Такое может произойти лишь в том случае, если при однократном действии этой трансформации волновая функция либо остается прежней, либо умножается на минус единицу. В первом случае она называется симметричной, во втором — антисимметричной.

Это вроде бы чисто математическое различие радикально влияет на, так сказать, возможности квантовой системы по части ее внутреннего устройства. При симметрии волновой функции любое число частиц может иметь одни и те же координаты, а при антисимметрии это невозможно. Логика тут простая. Перестановка двух частиц, имеющих одинаковые координаты, с одной стороны, не меняет квантовую систему, а с другой — меняет знак ее антисимметричной волновой функции. Следовательно, в этом случае все частицы должны располагаться в разных точках пространства. Это частный случай знаменитого принципа исключения (или принципа запрета), который в 1925 году сформулировал Вольфганг Паули по отношению к электронам.

Конечно, волновая функция может зависеть не только от координат частиц, но и еще от каких-то характеристик, определяющих их состояние — скажем, импульсов и угловых моментов. Поэтому общая формулировка принципа Паули утверждает, что если волновая функция меняет знак при перестановке наборов параметров, полностью определяющих квантовые состояния отдельных частиц, то в любом допустимом состоянии в каждый момент времени может находиться не более одной частицы. Возвращаясь к уже сказанному, легко видеть, что симметричные волновые функции описывают системы одинаковых бозонов, а антисимметричные — фермионов.

Как известно, в число параметров состояния квантовых частиц входят и их собственные моменты количества движения, они же спины. В 1940 году Вольфганг Паули математически доказал, что частицы с целым спином являются бозонами, а с полуцелым — фермионами. В начале 1970-х итальянский физик Сержио Доплишер вместе со своим немецким коллегой Рудольфом Хаагом и англичанином Джоном Элиасом Робертсом получили тот же результат как следствие постулатов аксиоматической квантовой теории поля.

Новые идеи

Приведенные выше аргументы долго считались непререкаемыми. Однако в 1977 году физики из Университета Осло Йон Лейнос и Ян Мюрхейм показали, что они строго обоснованы лишь в пространствах с тремя и более числом измерений². А вот для частиц и квазичастиц, замкнутых в одномерном или двумерном пространстве, эта логика уже не проходит. Если так, то априори нет оснований утверждать, что такие частицы могут быть исключительно бозонами или фермионами. Поэтому, как отмечено в их статье, «в одномерном или двумерном пространстве можно предположить существование систем, которые будут занимать промежуточное положение между бозонными и фермионными системами».

Я не знаю, в какой степени статья Лейноса и Мюрхейма подтолкнула мысль Вилчека, но, во всяком случае, он на нее ссылался. Как бы то ни было, он и ряд других физиков независимо друг от друга пришли к аналогичному выводу, в результате чего и появилась гипотеза энионов. Она утверждает, что двумерное движение приводит к появлению квазичастиц с числами заполнения, которые не ограничиваются нулем и единицей, как у фермионов, но и не могут иметь априори любую величину, как у бозонов. Хоть энионы и способны соседствовать в своих квантовых квартирах-состояниях, но количество соседей подчиняется определенным ограничениям.

В чем же состоит принципиальная разница между трехмерием и двумерием с точки зрения квантовой статистики? Пусть опять имеется система из какого-то числа одинаковых (в системе понятий квантовой механики — абсолютно неразличимых) частиц, две из которых меняются местами. В мире из трех (и большего числа) измерений этот обмен можно осуществить как движение по непересекающимся двумерным траекториям. То же самое относится и к обратному обмену, который возвращает частицы на их первоначальные места. Поэтому после такого парного обмена волновая функция всей системы или вообще не изменится (тогда мы имеем дело с бозонами), или поменяет знак (это фермионы). А вот в двумерии траектории при парных обменах могут пересекаться, что легко увидеть, если изобразить их на листе бумаги. Если допустить такие пересечения, то будет невозможно гарантировать, что после возвращение частиц волновая функция всей системы либо вернется к прежнему значению, либо изменит знак на противоположный.

Конечно, это только иллюстрация, и сама по себе она ровно ничего не доказывает. Однако она позволяет предположить — только предположить, — что обмены частиц в двумерном пространстве могут менять волновые функции более сложным образом, чем это имеет место в трехмерии и многомерии.

Чтобы это понять, взглянем на парные обмены частиц в двумерном пространстве (будем считать его евклидовой плоскостью) в квантовой перспективе. Для начала рассмотрим ситуацию, когда каждая частица уходит из своей позиции, один или несколько раз описывает замкнутую кривую (пусть для наглядности это будет окружность) и возвращается на прежнее место. Может показаться, что после таких перемещений волновая функция вообще не изменится, ведь обмена фактически не было. Так и будет, если окружности расположены в непересекающихся участках плоскости. А что произойдет, если одна окружность лежит внутри другой? В этом случае частицы повернутся относительно друг друга на какое-то целое число полных оборотов. Согласно общим принципам квантовой механики, это приведет к изменению фазы их волновой функции. Конкретно, ее прежнее значение умножится на e^iφ (здесь e — основание натуральных логарифмов, i — мнимая единица и φ — относительный угол поворота).

Казалось бы, это уточнение есть чистая формалистика. Как бы частицы не крутились по своим траекториям, угол φ всегда будет равен 2πn, где n — целое число. Как учат в школе, e^i2πn = 1. Таким образом, волновая функция умножится на единицу, следовательно, никак не изменится. Это и в самом деле так, но наши рассуждения только начались.

Теперь рассмотрим реальный парный обмен. Самая простая картинка — это движение двух частиц, которые первоначально находились на двух концах диаметра окружности, а затем сместились по двум полуокружностям навстречу друг другу. В этом случае угол их относительного поворота равен уже не 2π, а π. При множественных вращениях он будет равен π(2n + 1). Тогда волновую функцию надо будет умножить на е^{iπ(2n + 1)}, что всегда равно минус единице.

Здесь возникает естественный вопрос: к чему вся эта возня с картинками, которая вроде бы только наводит тень на плетень? Чтобы на него ответить, учтем, что угол относительного поворота задается параметром n, который остается неизменным при любых непрерывных деформациях траекторий, не ведущих к пересечению особой точки — центра вращения. На математическом языке этот угол является топологическим инвариантом. Совершив логический скачок, можно выдвинуть гипотезу, что в общем случае обмен частицами ведет к умножению волновой функции на e^ipφ, где p — произвольный параметр, который не обязан быть целым числом. В частности, самый элементарный обмен, при котором частицы поворачиваются на пол-оборота, приводит к фазовому множителю равному e^ipπ. Симметричные и антисимметричные волновые функции возникают только при выделенных значениях параметра p. Первым (то есть бозонным) соответствуют целые четные числа, вторым (фермионным) — нечетные.

Чтобы не умножать число символов, можно фазовый множитель записывать просто как e^iφ, считая, что φ может быть любым вещественным числом. Если оно кратно 2π, возникает статистика бозонов, если только π — фермионов. В остальных случаях имеем те самые промежуточные ситуации между бозонами и фермионами, о которых писали Лейнос и Мюрхейм. Именно такую возможность предположил Вильчек, когда выдвинул энионную гипотезу. Естественно, энионам нельзя приписать ни целый, ни полуцелый спин. Более того, нельзя даже априори утверждать, что повороты на один и тот же угол по часовой стрелке и против нее одинаково меняют волновую функцию эниона.

Теперь понятна и роль двумерия. В трехмерном пространстве все траектории, о которых только что шла речь, можно деформировать либо в несвязанные друг с другом точки, либо в элементарные двухчастичные обмены. Других топологических инвариантов здесь нет. Поэтому, в соответствии со сказанным выше, в трехмерии возможны только симметричные либо антисимметричные волновые функции, между которыми нет никаких промежуточных вариантов. Иначе говоря, никаких энионов.

В заключение этой темы чуть-чуть углублюсь в математику. Как опять-таки учат в школе, общее число перестановок N одинаковых объектов равно N! Любую такую перестановку можно разложить на какое-то число парных перестановок, которое будут или четным, или нечетным. Для каждой конкретной перестановки в принципе можно построить много таких разложений, но их четность всегда будет одинаковой. Если каждой четной перестановке поставить в соответствие единицу, а каждой нечетной — минус единицу, то весь набор возможных перестановок множества из N элементов отобразится только в эти два числа. Тем самым мы получим самое простое из всех возможных представление группы перестановок (так называемая группа S_n), отображающее все ее элементы только в два числа вещественной оси — единицу или минус единицу. Как уже говорилось, его результат зависит только от того, является ли число парных перестановок, на которые разлагается исходная множественная перестановка, четным или нечетным, но не от порядка (такие представления называются абелевыми). Именно это и является математической базой однозначного разделения волновых функций на симметричные и антисимметричные.

В случае энионов ситуация меняется. Напомню, что их перестановки описывают не простыми «перескоками» частиц, а их взаимными поворотами. При такой интерпретации переходы N одинаковых объектов друг в друга описываются не группой перестановок S_n, а совсем другой группой B_n — braid group («оплеточная» группа). Ее алгебра куда сложнее алгебры группы перестановок, и описывать ее я не берусь. Отмечу только, что сопоставление парным перестановкам частиц угла φ (а тем самым и фазового множителя e^iφ) является одномерным представлением этой группы, отображающим ее элементы на множество действительных чисел. У нее есть представления и высших размерностей, которым соответствуют более сложные типы квантовой статистики, где результаты парных перестановок зависят от их порядка (как легко предположить, такие представления именуются неабелевыми). На сегодня реальность простейшей (то есть абелевой) версии такой статистики уже продемонстрирована в экспериментах (впервые в 2020 году, см. ниже), в то время как ее неабелевы варианты пока не обнаружены. Однако в лабораториях их ищут, причем весьма упорно.

Представление об энионах возникает не только в физике конденсированных сред. Например, энионы появляются в релятивистской квантовой теории поля³. Они имеют место и в теории струн — но это уже совсем другая история.

Реальные двумерия

Фрэнк Вилчек выдвинул свою идею в чрезвычайно подходящее время. Именно тогда, в начале 1980-х годов, был обнаружен удивительно красивый твердотельный феномен — квантовый дробный эффект Холла. Его открытие и объяснение в 1998 году было удостоено Нобелевской премии по физике. Он имеет место (разумеется, при подходящих условиях) в случае двумерного движения электронов в поперечном магнитном поле при гелиевых температурах. Роль двумерия играет плоская поверхность раздела двух полупроводников с близкими кристаллическими структурами. Обычно это тонкие пленки арсенида галлия и арсенида алюминия-галлия, выращенные на кремниевой подложке посредством осаждения компонентов из разреженной газовой смеси (так называемой газофазной эпитаксии). Если магнитное поле очень сильно (более 10 тесла), электронный газ приобретает свойства практически несжимаемой квантовой жидкости. Эксперимент показал, что в этой жидкости возникают квантованные вихревые возбуждения, которые являются квазичастицами с эффективным дробным электрическим зарядом (напомним, что элементарная единица заряда — это заряд электрона e). Впервые этот эффект обнаружился для квазичастиц с зарядом e/3. Впоследствии были детектированы и другие заряды — например, 2/5 e и 4/9 e.

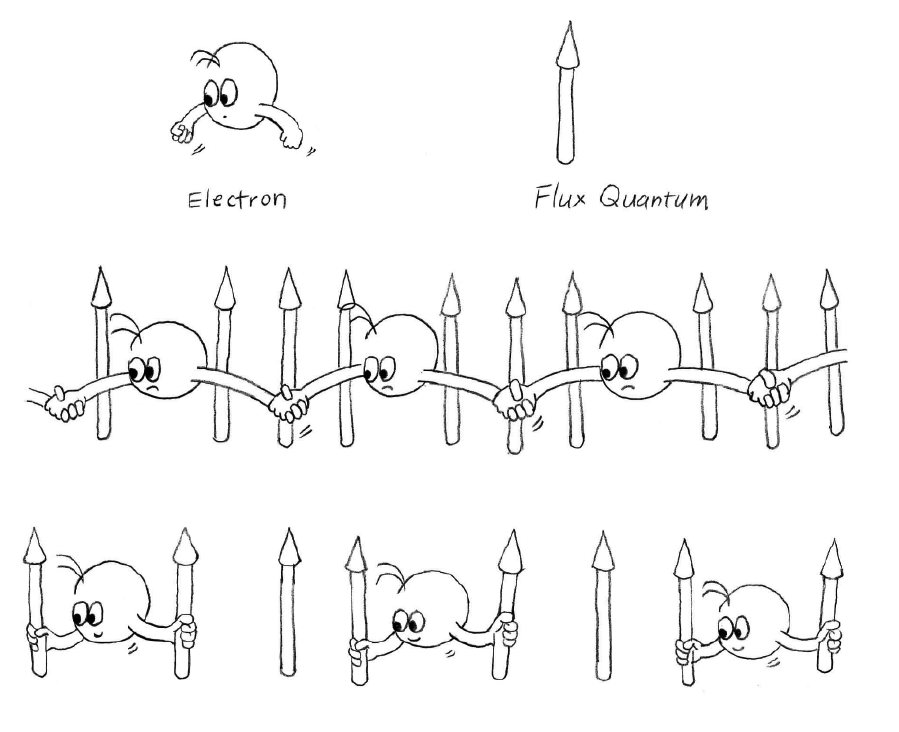
Причины возникновения дробного квантового эффекта Холла (кстати, чуть раньше был открыт более простой целочисленный эффект) довольно сложны, и здесь нет места о них рассказывать. Отмечу только, что его, в отличие от целочисленного эффекта, нельзя объяснить в терминах двумерных движений одиночных электронов в магнитном поле. Это принципиально многочастичный феномен, в основе которого лежат межэлектронные корреляции. Они приводят к тому, что электроны объединяются с квантами магнитного потока, в результате чего возникают композитные частицы, в чем-то напоминающие описанные выше структуры Вилчека. При этом электрон может объединиться с несколькими магнитными квантами — скажем, с тремя.

Такие союзы уменьшают межэлектронное кулоновское отталкивание, что можно интерпретировать как уменьшение электрического заряда. Поэтому композит с тремя квантами (с открытия которого, напомню, как раз и началось изучение дробного квантового эффекта Холла) ведет себя как частица, чей заряд втрое меньше электронного. Сами электроны, конечно, на части не делятся, но их заряды как бы расплываются в окружающем пространстве. При других составах электронно-магнитных композитов могут возникать более сложные ситуации, но и они поддаются объяснению.

Есть еще один момент, который просто нельзя не упомянуть. Присоединение вихревых квантов магнитного потока влияет на статистику квазичастиц. В частности, электрон с нечетным числом квантов (в том числе и с тремя) становится композитным бозоном. Этот процесс иногда называют квантовой трансмутацией. Он имеет множество интереснейших последствий, на которых я просто не могу останавливаться.

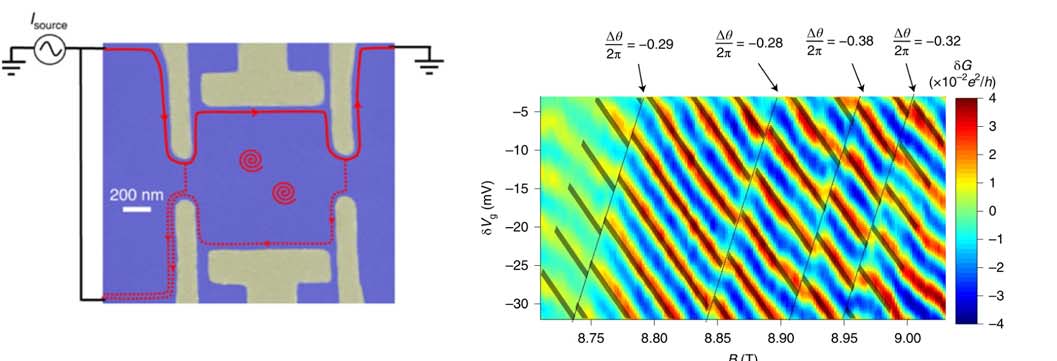
Теоретики давно предполагали, что квазичастицы с дробными зарядами могут обладать предсказанными теорией свойствами энионов и потому подчиняются «оплеточной» статистике. В 2020 году это впервые удалось продемонстрировать в двух различных по замыслу и исполнению экспериментах⁴. Анализ полученных результатов показал, что движение квазичастиц с дробными зарядами в каждой экспериментальной установке не согласуется ни с бозонной, ни с фермионной статистикой, однако вполне соответствует ожиданиям, основанным на теории энионов. Так что трансмутация электронов в композитные бозоны, о которой только что говорилось — это еще цветочки, есть вещи куда более парадоксальные.

Топологические компьютеры — фантазия или реальность?

Энионные системы считаются весьма перспективными носителями информации для будущих квантовых компьютеров. Если очень кратко, дело здесь в следующем. Как известно, ныне существующие образцы квантовых процессоров очень чувствительны ко всякого рода шумам, которые разрушают когерентные состояния кубитов. Тем самым они препятствуют сколько-нибудь длительной работе даже простых вычислительных алгоритмов, а также вынуждают изобретать сложные корректирующие программы.

Для энионов это ограничение если не снимается полностью, то значительно ослабляется. Причина в том, что взаимодействия между энионами регулируются топологией их мировых линий. Поэтому они не должны искажаться умеренными локальными возмущениями этих линий — т. е. не чувствовать разрушительного воздействия хотя бы слабых и не особо длительных шумов. Выражаясь иначе, квантовая информация, которая кодируется и считывается энионами, распределяется не локально, на отдельных кубитах, как в ныне существующих моделях, а глобально, по всей системе. Поэтому ее носители принято называть топологическими кубитами. Конечно, пока это теория, но разработчики квантовых процессоров надеются подтвердить ее на практике.

Квазичастицы с дробными зарядами — отнюдь не единственные кандидаты на роль «начинки» квантовых вычислителей. Фирма Microsoft уже несколько лет финансирует создание экспериментального квантового процессора, использующего квазичастичные аналоги так называемых майорановских фермионов. Существование этих частиц в теории вытекает из очень интересной реинтерпретации знаменитого уравнения Дирака, которую в 1937 году опубликовал чрезвычайно талантливый (и, увы, на следующий год бесследно исчезнувший, скорее всего, ушедший из жизни) итальянский физик Этторе Майорана⁵. Как известно, уравнение Дирака описывает массивную частицу с единичным отрицательным зарядом и половинным спином — т. е. релятивистский электрон. Оно имеет две модификации, носящие имена замечательного немецкого математика Германа Вейля (он также много лет работал в Швейцарии и США) и Этторе Майораны. Уравнение Вейля соответствует заряженному фермиону, а уравнение Майораны — незаряженному. Вейлевский фермион массы не имеет, а вот фермион Майораны может быть как безмассовым, так и массивным. Наконец, майорановские частицы обладают еще одним нетривиальным свойством — они являются своими собственными античастицами.

Квазичастичные аналоги майорановских фермионов в двумерном пространстве, обладающие близкой к нулю энергией, так называемые майорановские нулевые моды, тоже идентичны своим античастицам. При этом они являются неабелевыми энионами (то есть, подчиняются неабелевой статистике). Поэтому, согласно теории, они могут обеспечивать ту самую топологическую защиту от шумов, о которой говорилось выше⁶. Стоит отметить, что майорановские нулевые моды могут возникать и в одномерных системах. Конечно, там не может быть реальных «плетений», однако это препятствие преодолимо с помощью специальных математических приемов, на которых я не буду останавливаться.

Пока что майорановские нулевые моды существуют только на бумаге. Правда, результаты некоторых экспериментов позволяют заподозрить их реальность. Однако эти результаты, как правило, допускают и иные интерпретации, так что путь к открытию таких мод может оказаться долгим.

* * *

В заключение остановлюсь на совсем недавних событиях. 19 февраля 2025 года корпорация Microsoft объявила о создании прототипа компьютерного чипа с принципиально новой архитектурой, реализованной посредством алюминиевых нанопроводов на подложке из арсенида индия. Компания заявила, что работа этого устройства основана на генерации контролируемых квантовых возбуждений майорановского типа — иначе говоря, майорановских квазичастиц. В соответствии с этой заявкой, микропроцессору присвоено название Majorana1. Фирма полагает, что ее чип позволит получать более стабильные и лучше управляемые кубиты, нежели другие прототипы квантовых компьютерных систем.

Это сообщение⁷ одновременно появилось в корпоративном пресс-релизе и в журнале Nature. Однако уже на следующей неделе тот же журнал поместил материалы, где критиковалась малоинформативность сообщения и даже ставилась под сомнение сама возможность создания квантового компьютера на основе майорановских квазичастиц⁸. 20 марта о растущих сомнениях в отношении корректности претензий сотрудников Microsoft на создание майорановского процессора сообщил⁹ и журнал Science. Наконец 17 апреля в Nature появилась заметка, где это и другие сенсационные сообщения о якобы достигнутых необыкновенных возможностях квантовых вычислительных устройств названы «квантовым ажиотажем»¹⁰.

В общем, на данный момент дальнейшая судьба Majorana1 остается неясной. На этом позволю себе закончить.

Алексей Левин

¹ Wilczek F. Magnetic flux, angular momentum, and statistics // Physical Review Letters, 48, 1144 (1982); Wilczek F. Quantum mechanics of fractional-spinparticles // Physical Review Letters. 49, 957–59 (1982).

² Leinaas J. M. and Myrheim J. On the Theory of Identical Particles // Il Nuovo Cimento. Vol. 37B. N. 1, 1–23 (1977).

³ Schwartz M. D. Quantum Field Theory and the Standard Model. Cambridge University Press, Cambridge, 2014, p. 208–211.

⁴ Bartolomei H. et al., Fractional statistics in anyon collisions // Science, 368, 173–177 (2020); Nakamura J. et al., Direct observations of anionic braiding statistics // Nature Physics, 16, 931–936 (2020).

⁵ Предположения о том, что могло бы случиться с итальянским физиком, изложены в очерке Виталия Мацарского «Жизнь и антижизнь Этторе Майораны»: trv-science.ru/zhizn-i-antizhizn-fizika-ettore-majorany/

⁶ Yazdani A. et al. Hunting for Mayoranas // Science, 380, 1235–1246 (23 June 2023).

⁷ Microsoft Azure Quantum, Aghaee M., Alcaraz Ramirez A. et al. Interferometric single-shot parity measurement in InAs–Al hybrid devices // Nature 638, 651–655 (2025).

⁸ Castelvecchi D. Microsoft’s quantum chip leaves some physicists skeptical // Nature, 638, 872 (2025); Garisto D. Microsoft quantum-computing claim still lacks evidence: physicists are dubious // Nature, 18 March 2025.

⁹ Savitsky Z. Debate erupts around Microsoft’s blockbuster quantum computing claims // Science 387, 1338–1339.

¹⁰ Arrow J. Don’t believe the quantum hype // Nature, 640, 572 (17 April 2025).