

Международный коллектив специалистов по экспериментальной физике высоких энергий, работающих в американской Национальной ускорительной лаборатории им. Энрико Ферми, обнародовал новейшие результаты измерения аномального магнитного момента мюона, которые оказались в разумном согласии с результатами теоретических вычислений, выполненных на основе Стандартной модели элементарных частиц. Это означает, что Стандартная модель выдержала очередную проверку на прочность, дав возможность объяснить накопленные за последние годы экспериментальные данные по магнитным свойствам мюона без привлечения гипотез, выходящих за ее рамки (так называемой Новой Физики). Сообщение исследовательской группы Muon g–2 Collaboration, озаглавленное “Measurement of the Positive Muon Anomalous Magnetic Moment to 127 ppb”1, появилось в архиве электронных препринтов 2 июня и уже на следующий день было доложено на семинаре в Фермилабе, собравшем более тысячи участников. Эта информация также представлена в статье, направленной для публикации в журнал Physical Review Letters.
Споры вокруг измерения и теоретического объяснения аномальных магнитных моментов заряженных элементарных частиц семейства лептонов — электрона, мюона и тау-лептона — имеют почти что вековую историю. Ее полезно знать, чтобы лучше разобраться в современной проблеме мюонного магнетизма.
Вступительная физика
Истоки этой проблемы лежат в полученном еще в XIX веке результате классической электродинамики, согласно которому замкнутый контур с током ведет себя как магнитный диполь. Отсюда следует, что он обладает векторным магнитным моментом, который перпендикулярен его плоскости (если контур плоский). Численная величина этого момента равна произведению площади контура на силу тока. В магнитном поле такой контур приобретает потенциальную энергию, равную скалярному произведению его магнитного момента на напряженность (точнее, индукцию) поля, взятому с обратным знаком. Поэтому свободно подвешенная рамка с током поворачивается в однородном магнитном поле таким образом, что вектор ее магнитного момента ориентируется параллельно вектору напряженности поля. Именно при такой конфигурации ее потенциальная энергия достигает минимума, и рамка устанавливается в положении устойчивого равновесия.
Пока что речь шла о классической науке. Через несколько лет после того, как Макс Планк в 1900 году опубликовал свою квантовую гипотезу, некоторые физики стали допускать существование не только квантов энергии, но и квантов (то есть элементарных и неделимых порций) магнитных моментов, тоже связанных с постоянной Планка. В полной мере квантованные магнитные моменты электронов вошли в физику вместе с планетарной моделью водородоподобного атома, предложенной в 1913 году Нильсом Бором. Как известно, в этой модели электроны фигурируют в качестве точечных заряженных частиц, которые обращаются вокруг ядра по классическим орбитам. Однако набор этих орбит дискретен, причем каждой соответствует определенный уровень энергии находящегося на ней электрона. Заселенные орбиты превращаются в витки с электрическим током и, следовательно, обретают магнитные моменты.
Бор показал, что в его модели магнитные моменты орбитальных электронов действительно квантуются подобно их энергии. Отсюда следует, что магнитный момент электрона на любой орбите равен целому числу своих элементарных единиц, магнитных квантов, причем величина кванта равна магнитному моменту электрона на ближайшей к ядру орбите. В 1920 году Вольфганг Паули назвал этот квант магнетоном Бора. Его формула зависит от системы единиц; например, в системе СИ магнетон Бора μB равен eħ/(2mec), где e — заряд электрона, ħ — приведенная постоянная Планка, me — масса электрона, а с — скорость света.
Как известно, в нерелятивистской квантовой механике динамика электрона описывается уравнением Шрёдингера, которое связывает производную от его волновой функции по времени с действием на ту же функцию оператора энергии, он же гамильтониан. Если электрон находится в тех или иных силовых полях, гамильтониан включает как оператор кинетической энергии свободного электрона, так и дополнительные слагаемые, описывающие эти поля. В частности, уравнение Шрёдингера для единственного электрона атома водорода, находящегося во внешнем магнитном поле, включает в качестве одного из этих слагаемых оператор электростатического (кулоновского) поля ядра, а другим — квантовую версию уже упоминавшейся классической добавки к потенциальной энергии, вызванной взаимодействием магнитного момента с этим полем (имеется в виду момент электронной орбиты). Она равна магнетону Бора, умноженному на скалярное произведение оператора полного углового момента электрона L на напряженность магнитного поля B (поскольку оба сомножителя — векторы, они обозначены жирным шрифтом). Таким образом, этот член гамильтониана записывается как μB · B · L. На всякий случай напомню, что скалярное произведение B · L в декартовых координатах выглядит как BxLx + ByLy+BzLz.
Однако в таком виде этот гамильтониан продержался недолго. Как только было доказано, что электрон обладает внутренним (спиновым) угловым моментом (см. об этом мою статью «Вольфганг Паули: спин, спиноры и всё такое»2), у гамильтониана появился еще один член с похожей, но не полностью идентичной структурой. Магнетон Бора в нем умножается не только на скалярное произведение оператора спина S на вектор напряженности магнитного поля, но и на новую константу ge, так называемое гиромагнитное отношение электрона. Поэтому в окончательном виде «магнитная» добавка к гамильтониану выглядит сложнее: μB · B · (L + ge · S). Точности ради отмечу, что так ее записывают в наше время, раньше использовались другие обозначения. Впрочем, сути дела это не меняет.
Уравнение Шрёдингера (точнее, вся нерелятивистская квантовая механика) никак не предписывает численную величину гиромагнитного отношения ge. Оно выступает просто как свободный параметр, который должен определяться на основе экспериментов. Ситуация радикально изменилась, когда Поль Дирак в 1928 году нашел свое знаменитое релятивистское уравнение электрона. Из него автоматически вытекает, что в единицах приведенной постоянной Планка спин электрона равен ½ (в полной записи ½ · ħ), а его гиромагнитное отношение равно в точности двум, ge = 2. Это очень изящный результат, который по праву считается одним из самых блестящих предсказаний теоретической физики первой половины прошлого столетия.
Появление аномалии
В 1930-е годы дираковское значение гиромагнитного отношения в общем принималось на веру и практически не подвергалось проверке. Во всяком случае, мне известен только один результат эксперимента по изучению эффекта Зеемана в неоне, выполненного в Физической лаборатории им. Нормана Бриджа Калифорнийского технологического института, который подтвердил, что ge с некоторыми натяжками можно считать равным двум3. Однако следует учесть, что точность спектроскопических измерений тогда была относительно невелика. После Второй мировой войны она значительно повысилась за счет применения новых микроволновых технологий, разработанных при создании радиолокаторов. В итоге в 1947 году сразу две небольшие группы американских физиков сообщили, что гиромагнитная постоянная электрона несколько превышает двойку4. Хотя оцененная в их экспериментах численная величина разности ge — 2 приблизительно равнялась всего лишь двум тысячным, всё же несовпадение с дираковским значением было несомненным. Стоит отметить, что одним из авторов первой статьи был лауреат Нобелевской премии 1944 года профессор Колумбийского университета Исидор Раби, а второе исследование выполнил профессор того же университета и будущий нобелиат Поликарп Куш, который работал вместе со своим коллегой по физическому факультету Генри Фоли. Куш получил Нобелевскую премию в 1955 году как раз за точное измерение магнитного момента электрона.
Интересно, что в том же 1947 году другие физики из Колумбийского университета опубликовали еще один результат нобелевского класса, указавший на границы применимости уравнения Дирака. Согласно этому уравнению, два состояния электронов атома водорода, имеющих одно и то же главное квантовое число и один и тот же полный угловой момент, но отличающиеся величиной орбитального момента, должны иметь одинаковую энергию. Экспериментаторы поставили этот прогноз под сомнение еще в предвоенные годы, однако проблема тогда решена не была. С ней разделался профессор Уиллис Лэмб, который работал вместе со своим аспирантом Робертом Ризерфордом. Используя новые возможности микроволновых технологий, они показали, что энергия уровня 2S1/2 превышает энергию уровня 2P1/2 на 1051 мегагерц, что почти равно современному значению 1054 мегагерц. За открытие этого эффекта, названного лэмбовским сдвигом, Лэмб в 1955 году разделил с Кушем Нобелевскую премию.
Таким образом, через два года после окончания Второй мировой войны в лабораториях Колумбийского университета была продемонстрирована настоятельная необходимость корректировки не только уравнения Дирака, но и всей релятивистской теории взаимодействия электронов с фотонами, созданной в 1920-х–1930-х годах. Впрочем, теоретики осознали эту необходимость даже раньше. Математический аппарат довоенных вычислений электронно-фотонных процессов неустранимо порождал не имеющие физического смысла бесконечности и потому явно требовал изменений. К слову, Роберт Оппенгеймер тогда воспринял эти бесконечности настолько трагически, что в опубликованной в 1930 году статье вообще усомнился в возможности построить последовательно релятивистское описание взаимодействия электронов и фотонов.
К счастью, его опасения не оправдались. В завершенном виде последовательно релятивистская теория электромагнетизма, квантовая электродинамика, все же появилась на свет — во второй половине 1940-х годов. Ее создателями стали американцы Джулиан Сеймур Швингер и Ричард Филлипс Фейнман, а также японский физик-теоретик Синъитиро Томонага, который пришел к этой теории еще в 1943 году. В 1965 году все трое были награждены Нобелевскими премиями.
В 1948 году Швингер, Фейнман и Томонага независимо друг от друга объяснили лэмбовский сдвиг, связав его с квантовыми флуктуациями вакуума — фотонного и электрон-позитронного полей, которые искажают кулоновский потенциал атомного ядра и тем самым меняют потенциальную энергию взаимодействия ядра и электрона. Также удалось посчитать теоретическую величину этого сдвига, которая хорошо совпала с результатами Лэмба. Аномальный магнитный момент электрона (то есть отличие его гиромагнитного отношения от дираковского значения) тоже возникает из-за рождения различных виртуальных частиц, которые создают так называемые радиационные поправки к дираковскому значению. Это было впервые вычислено Швингером даже раньше, в конце 1947 года, и тогда же результат опубликован (правда, деталями своих чрезвычайно сложных вычислений Швингер поделился только в 1948–1949 годах). Вскоре к тому же результату пришли Фейнман и Томонага. Они разными способами показали, что в первом порядке теории возмущений ge = 2 + α/π, где α — безразмерный параметр, приблизительно равный 1/137 (его историческое название — постоянная тонкой структуры). В квантовой электродинамике он определяет силу взаимодействия между заряженными частицами и фотонами как переносчиками электромагнитного взаимодействия.
Вычисления Швингера и других создателей квантовой электродинамики установили численную величину главной поправки к дираковскому значению гиромагнитного отношения, пропорциональной первой степени постоянной тонкой структуры. Как оказалось, она равна 0,00232. Позднее теоретики вычислили поправки меньшего масштаба, пропорциональные второй, третьей и четвертой степеням постоянной тонкой структуры. Все эти вычисления были сделаны на базе математического аппарата одной только квантовой электродинамики, т. е. без помощи теории кварков и теории слабых взаимодействий. В результате этих усилий и многочисленных результатов экспериментаторов магнитный момент электрона сейчас известен с совершенно фантастической точностью — аж до тринадцатого десятичного знака.
Гиромагнитное отношение принято записывать в виде g = 2(1+a), причем параметр а как раз и называют аномальным магнитным моментом (или просто магнитной аномалией). Иначе говоря,
а = (g–2)/2. Так что, согласно этому определению, магнитная аномалия электрона ae в первом приближении теории возмущений равна α/2π, т. е. 0,00116. Если бы мы захотели записать исправленное в первом приближении по α значение самого магнитного момента электрона μe, а не его гиромагнитного отношения, то там фигурировала бы именно она: μe = μB(1 + α/2π). Швингер так ценил свое вычисление аномального магнитного момента электрона, что завещал выбить формулу α/2π на своем надгробии, что и было сделано. Кстати, выражение для магнитного момента электрона, вычисленного во втором порядке теории возмущений, выглядит так: μe = μB(1 + α/2π — 0,328 · α2/π2). Как видим, вторая поправка не увеличивает магнитный момент, а уменьшает. В этом есть весьма нетривиальная сермяжная правда, но на ней я не буду останавливаться.

Переходим к мюонам
В 1947 году (опять в 1947-м!) было сделано теоретическое открытие, сделавшее возможным появление физики мюонов. Напомню, что эту частицу в эксперименте впервые обнаружили сотрудник Калтеха (и первооткрыватель позитрона!) Карл Андерсон и его аспирант Сет Неддермейер. Работая в 1936 году в горной лаборатории на высоте 4300 м, они заметили треки частиц, которые вели себя наподобие электронов, но явно были много массивней — где-то на два порядка. Через год такие же треки наблюдали физики из Гарварда и токийского Института физических и химических исследований.
Тогдашние эксперименты позволили оценить массу новооткрытой частицы лишь очень приблизительно — от 100 до 400 масс электрона. Как сейчас известно, она приблизительно в 207 (точнее, в 206,768) раз массивней электрона. Ее первое время отождествляли с предсказанными Хидэки Юкавой мезонами, носителями внутриядерных сил. Однако в 1947 году американские физики Роберт Маршак и Ганс Бете на основе анализа результатов ряда экспериментов 1940-х годов пришли к выводу, что это принципиально разные частицы5. Интересно, что такую же модель пятью годами ранее разработали японские физики Сёити Саката, Такэси Иноуэ и Ясутака Таникава, но английские переводы их статей дошли до США лишь в конце всё того же 1947 года. Сначала юкавскую частицу называли пи-мезоном, а «тяжелый электрон» Андерсона — мю-мезоном, потом появились современные названия — пион и мюон.
В 1950-е годы физики провели первую классификацию известных к тому времени элементарных частиц (точнее, тех частиц, которые тогда считали элементарными). Электрон, мюон и нейтрино вместе с их античастицами отнесли к категории лептонов (от греческого λεπτός — легкий), а прочие частицы разделили на два класса. Протон, нейтрон и все частицы большей массы назвали барионами (βαρύς — тяжелый). Термины «лептон» и «барион» в 1953 году придумал профессор принстонского Института перспективных исследований Абрахам Пайс, блестящий физик-теоретик и позднее крупный историк науки. Слово «мезон» (μέσος — средний) существовало с конца 1930-х годов, в эту категорию вошли пионы и открытые в начале 1950-х годов каоны. Фотон остался сам по себе как единственный представитель квантов электромагнитного поля. Тридцатка частиц конца 1950-х как раз и состояла из фотона, шести лептонов, семи мезонов и шестнадцати барионов. Если бы тогда было известно, что распады мюонов рождают два вида нейтрино, шестерка лептонов увеличилась бы до восьмерки. Однако мюонные нейтрино были открыты только в 1962 году.
Поскольку мюоны отличаются от электронов только массой и нестабильностью (они распадаются на электроны, позитроны и нейтрино), их динамика тоже описывается уравнением Дирака. Поэтому после окончательной идентификации мюонов было естественно предположить, что они обладают магнитными моментами с приблизительно таким же гиромагнитным отношением gμ и, соответственно, такой же магнитной аномалией aμ. Разумеется, единицей магнитного момента мюона должен служить аналог магнетона Бора, в котором электронная масса заменена на мюонную (и поэтому мюонный магнетон в 207 раза меньше электронного). Однако измерять магнитный момент мюона гораздо труднее, чем электронный, — прежде всего из-за нестабильности этой частицы. На сегодняшний день величина магнитной аномалии электрона ae установлена приблизительно в тысячу раз точнее, нежели величина aμ.
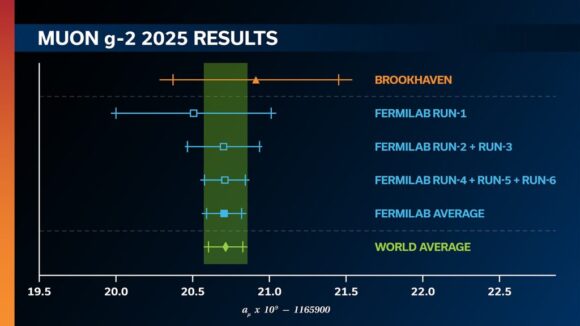
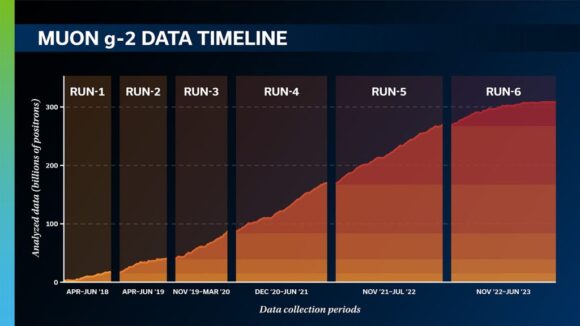
Первые эксперименты по определению магнитного момента мюона были предприняты во второй половине 1950-х годов в Ливерпульском и Колумбийском университетах, затем в течение следующих двух десятилетий систематически продолжены в ЦЕРНе. Потом эстафета перешла к Брукхейвенской национальной лаборатории, где измерения магнитного момента мюона проводились с 1997 по 2001 год. Ее финальный отчет6 был обнародован в 2006 году. Позднее этот эксперимент был перенесен в Фермилаб, для чего в 2013 году туда посредством сложной транспортной операции перевезли с Лонг-Айленда сверхпроводящее накопительные кольцо, внутри которого в ходе экспериментов циркулировали мюонные сгустки, рожденные при распаде пионов.
Я не буду вдаваться в описание технических деталей эксперимента в Фермилабе, поскольку их легко можно найти на сайте коллаборации7. Отмечу только, что появившиеся в 2018 году результаты первой серии фермилабовских измерений в целом подтвердили брукхейвенскую информацию.
Только что обнародованные данные представляют собой итоги обработки результатов второй и третий серий измерений магнитного момента мюона, которые проводились в Фермилабе в течение 2020–2023 годов. По точности они в четыре раза превосходят результаты предшествующих экспериментов. Откорректированное значение магнитной аномалии мюона дает aμ = 0,001165920705. Погрешность этой оценки не превышает 127 миллиардных долей.

Почему это сообщение вызвало такой интерес? Дело в том, что в недавнем прошлом экспериментальные данные по мюонной аномалии расходились с итогами ее теоретических вычислений настолько, что это могло вызвать беспокойство. Надо сказать, что эти вычисления были и остаются в высшей степени непростыми. Радиационные поправки к магнитному моменту электрона, как я уже отметил, вычисляются только с учетом виртуальных электронов, позитронов и фотонов. Для мюона этого недостаточно — надо принимать в расчет виртуальные частицы, участвующие в сильном и слабом взаимодействии. Техника таких вычислений исключительно сложна и трудоемка. Хотя прошлые результаты экспериментов и компьютерной симуляции не совпадали в сущей малости, они всё же позволяли предположить, что для их объяснения понадобится выход за рамки Стандартной модели. Например, вероятность случайного расхождения между результатами измерений в Брукхейвене и тогдашними теоретическими вычислениями составила 3,7 стандартного отклонения (как еще говорят, 3,7 σ). Она не дотянула до принятой в физике частиц нормы в 5 σ, достижение которой позволило бы говорить о реальном открытии, но всё же была слишком заметна, чтобы ею можно было просто пренебречь.
Сейчас ситуация изменилась. 27 мая (всего за шесть дней до публикации отчета Фермилаба!) созданная в 2017 году коллаборация физиков-теоретиков и экспериментаторов Muon g–2 Theory Initiative обнародовала8 новую собственную оценку магнитной аномалии мюона aμSM, полученную на основе Стандартной модели. Она равна 0,00116592033 — следовательно, отличается от оценки Фермила всего лишь приблизительно на четвертую часть одной миллиардной. Правда, погрешность для нее вчетверо больше, 530 миллиардных долей. Как бы то ни было, в авторской аннотации к огромному (188 страниц, 83 графических включения) материалу коллаборации Muon g–2 Theory Initiative утверждается, что «на современном уровне точности нет противоречий между Стандартной моделью и экспериментом». В то же время в заключительном разделе авторы подчеркивают важность новых экспериментальных и теоретических исследований, связанных с аномальным магнитным моментом мюона, которые и в дальнейшем будут полезны для проверки Стандартной модели.
Но это дело будущего. Эксперимент Muon g–2 в Фермилабе закончен, и, как сообщается, планы его возобновления отсутствуют. А пока Стандартная модель элементарных частиц полностью сохраняет свои позиции. У некоторых членов физического сообщества это вызывает разочарование, поскольку еще одна тропинка к Новой Физике привела к тупику. Но многие довольны: модель не подвела, и ею можно пользоваться без опасений. А что будет дальше — время покажет.
Позволю себе два заключительных замечания. Во-первых, для вычисления магнитной аномалии мюона очень важно иметь как можно более точную информацию об эффективных сечениях процессов аннигиляции электрон-позитронных пар, приводящих к рождению различных видов адронов. Такие измерения в последние годы интенсивно проводились на электрон-позитронном коллайдере ВЭПП-2000, действующем в Институте ядерной физики СО РАН. Их результаты сильно помогли корректировке теоретического значения этой аномалии участниками коллаборации Muon g–2 Theory Initiative.

Второе замечание из другой оперы. В контексте современных знаний о природе элементарных частиц термин «аномальный магнитный момент» выглядит как-то странновато. Добавка к дираковскому значению гиромагнитного отношения вызвана возмущениями физического вакуума, которые абсолютно закономерны и потому вполне нормальны. Аномалия имела бы место, если бы промеренные со всё большей точностью значения этого параметра не уходили от двух. Вот это было бы странно и требовало бы объяснения. Впрочем, это отнюдь не единственный анахронизм, сохранившийся в физической терминологии.
Алексей Левин
1 muon-g-2.fnal.gov/result2025.pdf
2 www.trv-science.ru/2025/01/wolfgang-pauli-spin-spinory-i-vsyo-takoe/
3 Kinster L.E. and Houston W. V. The Value of e/m from the Zeeman Effect // Physical Review, 45, 104 (15 January 1934)
4 Nafe J.E., Nelson E. B., and Rabi I. I. Hyperfine structure of atomic hydrogen and deuterium // Physical Review, 71, 914–15 (1947);
Kusch P. and Foley H. M. Precision measurement of the ratio of the atomic «g values» of the 2P3/2 and 2P1/2 states of gallium // Physical Review, 72, 1256–57 (1947).
5 Marshak R.E. and Bethe H. A. On the two-meson hypothesis // Physical Review, 72, 506 (1947).
6 Bennett G.W. et al. Final report of the E821 muon anomalous magnetic moment measurement at BNL // Physical Review D, 73, 072003 (7 April 2006).
7 muon-g-2.fnal.gov
elementy.ru/novosti_nauki/433800/Novye_rezultaty_obostryayut_i_zaputyvayut_zagadku_anomalnogo_magnitnogo_momenta_myuona

«например, в системе СИ магнетон Бора μB равен eħ/(2mec)» — описка: это система СГС; в СИ отсутствует «c» в знаменателе.