Радуга — красивейшее природное явление. И хотя видел ее практически каждый, мало кто может внятно объяснить причину ее появления. Не каждый сможет даже с уверенностью сказать, куда при наблюдении радуги светит солнце — в лицо или в спину. В этой статье мы расскажем, как образуется радуга и как радужное рассеяние проявляется в разных областях физики.
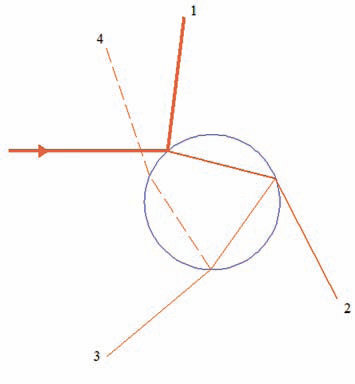
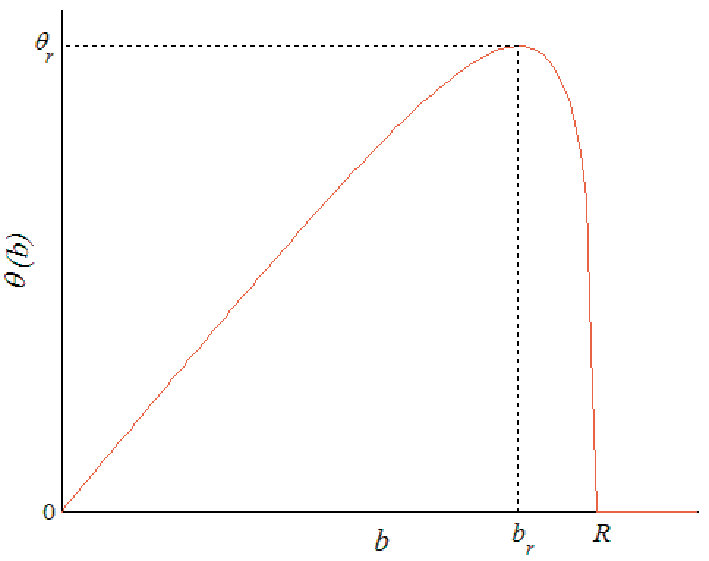
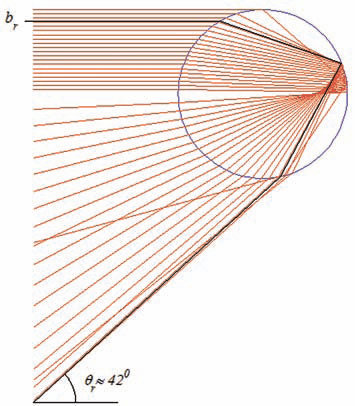
1. Свет, упавший на каплю воды, может отразиться от ее поверхности (рис. 1, линия 1), преломиться на границе, пройти внутрь капли, снова преломиться и выйти наружу (2) или же претерпеть внутреннее отражение и только после этого покинуть каплю (3). Именно эта третья ветвь функции отклонения луча обладает важным свойством: угол рассеяния достигает экстремума при некотором не равном нулю значении прицельного расстояния br (рис. 2). Именно такое поведение приводит к возникновению радужного рассеяния: световые лучи будут сгущаться по мере приближения угла рассеяния к углу радуги Qr , а область Q > Qr будет соответствовать геометрической тени (рис. 3, 4). Для водяной капли в воздухе этот угол составляет приблизительно 42°. Таким образом, капля, подсвеченная солнцем, будет ярко «светить» назад по образующей конуса с соответствующим углом раствора. Свет, исходящий от таких капель, создаст для находящегося в подходящем месте наблюдателя яркую дугу.
2. Цветная радуга обусловлена небольшим различием в показателе преломления воды для различных длин световых волн. Соответственно, точное значение угла радуги Qr также будет немного отличаться.
3. Иногда на небе можно увидеть две радуги (рис. 5). Радугу второго порядка порождает четвертая ветвь функции отклонения светового луча (линия 4 на рис. 1). Яркость радуги второго порядка будет меньше, а чередование цветов — обратным по отношению к основной радуге.
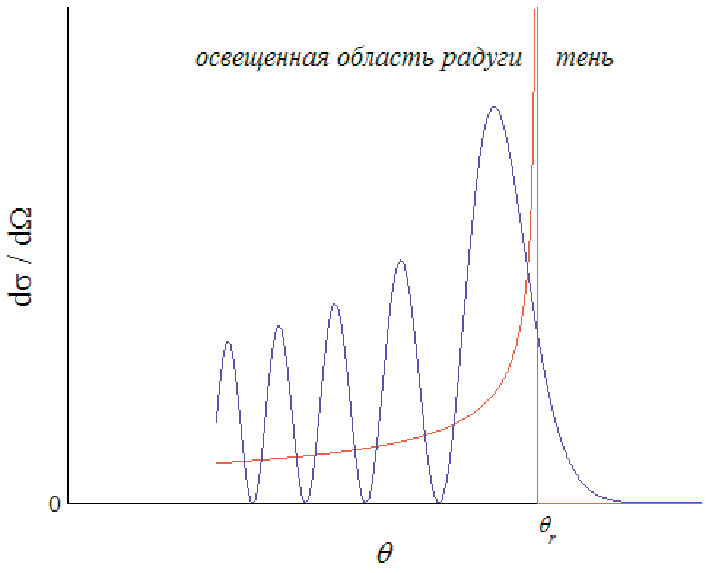
4. Учет волновых свойств света несколько усложняет картину. Поскольку на один и тот же угол Q > Qr будут рассеиваться два луча с различными прицельными расстояниями, между ними возникнет интерференция, приводящая к появлению осцилляций интенсивности (синяя кривая на рис. 4). Кроме того, за счет дифракционных эффектов рассеяние будет происходить и в область геометрической тени Q > Qr.

5. Попытки понять природу радуги предпринимались с древнейших времен. Создателем геометрической теории радуги следует, видимо, считать Рене Декарта, который первым продемонстрировал факт сгущения лучей при Q, стремящемся к Qr (1637 год). Количественную теорию радуги на основе волновой оптики построил в 1838 году английский астроном Дж Эйри. И хотя в области дополнительных радужных максимумов предсказания теории Эйри существенно отличаются от результатов разработанной в XX веке точной теории радуги, функция Эйри нашла применение в математической физике и, в частности, в квантовой механике.
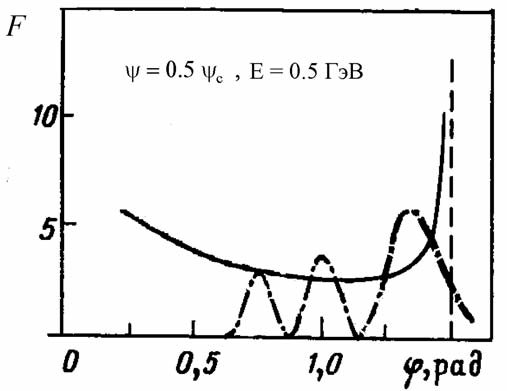
6. Рассеяние частиц формально ничем не отличается от рассеяния световых лучей, поэтому радужное рассеяние возможно не только в оптике, но и в механике. Необходимое условие возникновения радуги остается прежним: наличие экстремума в функции отклонения Q (b). Пример радужного рассеяния электронов на цепочке атомов показан на рис. 6.
7. Волновые свойства, присущие частицам в квантовой механике, усиливают сходство с оптикой. Первыми на возможность радужного рассеяния в атомных и ядерных столкновениях обратили внимание К. Форд и Дж. Уилер в статьях [1, 2]. В частности, ядерная радуга наблюдается при рассеянии легких ядер с энергиями 25-30 МэВ/нуклон средними и тяжелыми ядрами [4, 5].
Изложение теории радуги зачастую отсутствует даже в весьма солидных учебниках оптики. В свое время автору этих строк пришлось разбираться в предмете по популярным статьям [7-9] и монографии [10]. Зато с завидной регулярностью в периодике появляются обзоры по радуге, в том числе ядерной (см., например, [4-6]).
Владислав Сыщенко,
докт. физ-мат. наук,
Белгородский государственный
национальный исследовательский университет
1. Ford K.W., Wheeler J.A. Semiclassical description of scattering // Ann. of Phys. 7 (1959) 259-286 (reprinted in Ann. of Phys. 281 (2000) 608635).
2. Ford K.W., Wheeler J.A. Application of semiclassical scattering analysis // Ann. of Phys. 7 (1959) 287-322.
3. Ахиезер А.И., Шульга Н.Ф. Электродинамика высоких энергий в веществе. — М., Наука, 1993. — С. 155.
4. Ogloblin A.A. et al. Nuclear Rainbow in Scattering and Reactions and Nucleus-Nucleus Interaction at Small Distances // ЯФ 66 (2003) 1523 — 1533.
5. Khoa D.T. et al. Nuclear rainbow scattering and nucleus-nucleus potential // J. Phys. G: Nucl. Part. Phys. 34 (2007) R111.
6. Adam J.A. The mathematical physics of rainbows and glories // Phys. Rep. 356 (2002) 229-365.
7. Нуссенцвейг Х. Теория радуги // УФН 125 (1978) 527—547.
8. Пономарев Л.И. Числа радуги // Химия и жизнь, 1981, № 10, с. 44-50.
9. Трифонов Е.Д. Еще раз о радуге // Соросовский образовательный журнал, 2000, № 7, с. 53-58.
10. Ньютон Р. Теория рассеяния волн и частиц. — М., Мир, 1985. — 279 с.