Диалоги профессора Холмсона и доцента Ватсона о научной криминалистике

Кто стрелял первым, или с-криминалистика

— Увы, ничего интересного на этот раз, — разочарованно произнес профессор Холмсон, отложив в сторону новый выпуск «Успехов физических наук».¹

Ватсон прочитал название журнала и изумленно воскликнул:

— Что это вы читаете?!

— Тут обзор по струнным — и весьма странным — теориям…

— Но, профессор, с каких пор вас интересуют такие вещи? Когда мы познакомились, я с удивлением обнаружил, что вы понятия не имеете о вращении Земли вокруг Солнца. А вы сказали, что стараетесь забывать ненужные сведения. И сравнили мозг с маловместительным чердаком.

— Дорогой Ватсон, заметьте, я говорил о ненужных сведениях. Чтобы вы лучше поняли меня, расскажу вам о деле, по поводу которого мне пришлось недавно побывать в Штатах.

Случай, на первый взгляд, заурядный. По шоссе во встречных потоках мчались навстречу друг другу два автомобиля. Когда они сблизились, раздались выстрелы. Завизжали тормоза, выскочившие из других машин водители подбежали к виновникам, а точнее, к виновницам происшествия. Да, Ватсон, из автомобилей извлекли два прелестных создания в облегающих джинсах — на одной алая блузка, на другой белая. В дальнейшем этих девиц я буду именовать буквами А и Б по цвету их блузок, хотя их имена — Роз Мэдлав и Роз Крэзифил — выразительнее.

Дело казалось простым. Очевидцев хватало, чтобы выяснить, кто стрелял первым. Однако половина их были уверены, что первой стреляла мисс Б, а остальные — что Б лишь ответила на выстрел А. При этом все свидетели уверяли, что между выстрелами прошло нескольких секунд. Свидетелей виновности А было больше, и следователь заподозрил их сговор с Б. Он углубился в их биографии, но ничего определенного не нашел.

Тогда меня и попросили помочь. Опросив свидетелей еще раз, я обнаружил, что все, считавшие виновной А, ехали с ней в одном направлении, а все остальные — в противоположном. Вот и всё.

— Что всё? — удивленно спросил Ватсон.

— Да вот, взгляните, — и Холмсон протянул Ватсону свежую газету. На первой полосе крупными буквами было напечатано: «Р. Мэдлав и Р. Крэзифил обвинены в покушении на убийство друг друга».

— Простите, Холмс, но я решительно ничего не понимаю!

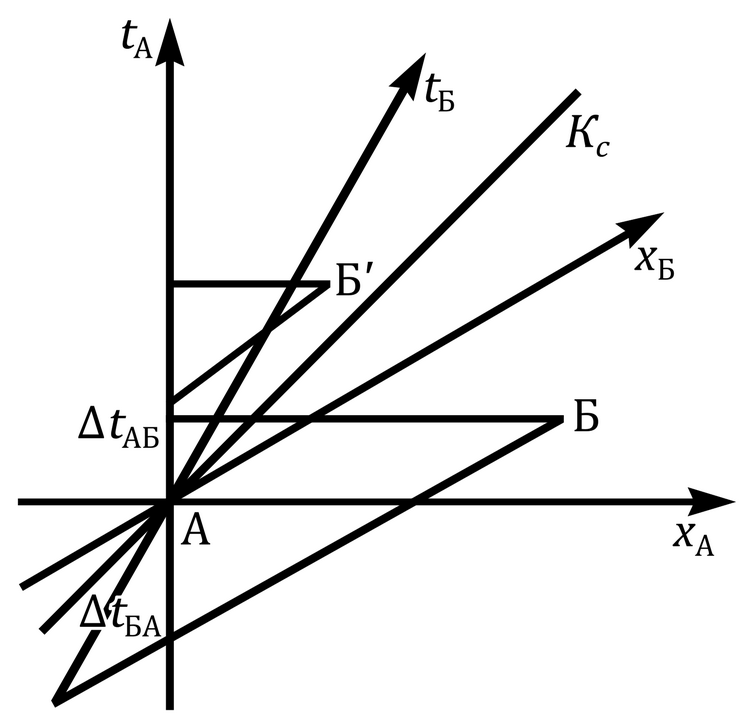
— Ну, что ж, извольте, поясню. Чтобы обойтись без формул, взгляните на рисунок, который я использовал в докладе для американских юристов «Теория относительности в криминалистике». На рисунке точками А и Б изображены интересующие нас события — выстрелы А и Б в пространстве-времени каждой из них. Начала систем отсчета совмещены с выстрелом А. Для свидетеля, который сидел бы в машине А или ехал бы рядом с ней, выстрел Б произошел через время Δt_AБ после выстрела А (точка Б проецируется на t_A параллельно х_А). Для свидетеля, который ехал рядом с Б, как следует из теории относительности, выстрел А произошел через время Δt_БA после выстрела Б (точка Б проецируется на ось t_Б параллельно х_Б). Таким образом, юридически оба выстрела были первыми.

— А если бы мисс Б действительно выстрелила после того, как услышала выстрел, то и тогда нашелся бы свидетель, для которого А выстрелила раньше Б?

— Нет, Ватсон, в этом случае выстрел Б изобразился бы точкой Б‘ внутри светового конуса, и, как легко видеть, для любого свидетеля, т. е. для любого угла осей с прямой Кс (прямые Кс образуют световой конус — все события, соответствующие приходу вспышки света из А) выстрел А предшествует выстрела Б‘; меняться может только интервал времени между выстрелами.

— Да, профессор, пожалуй, Фрэнсис Бэкон был прав, утверждая, что знание — сила.

— К сожалению, в обвинении отсутствует важный пункт.

— ???

— Превышение скорости. Ведь она отличалась от скорости света лишь на какую-то стомиллионную долю.

Ватсон после паузы, явно пытаясь что-то вспомнить, довольно улыбнулся и добавил:

— Наверняка обвинение пропустило еще один пункт: водители проскакивали красный свет светофоров. Ведь на такой скорости, благодаря эффекту Доплера, красный свет становится зеленым!

— Нет, Ватсон, это уж перебор. Вы не учли один важный, хоть и не физический факт, — на скоростном шоссе светофоров не бывает.

Как попасть в пятно Пуассона, или h-криминалистика

Доцент Ватсон, на правах друга ворвавшийся без доклада, застал профессора Холмсона играющим на скрипке. И нетерпеливо кашлянул:

— Как поживаете, профессор? Тот вздохнул и опустил смычок:

— Скверно, Ватсон. Замучили посетители…

Не заметив шпильки, Ватсон с жаром воскликнул:

— Должен вам сказать, профессор, жизнь полна удивительных совпадений!

— Не могу с вами не согласиться, — Холмсон искоса посмотрел на друга. — Всякий раз, когда я беру в руки скрипку, приходите вы и начинаете кашлять.

— Прошу прощения, — не смутился Ватсон, — но мой случай гораздо интересней! Только вчера я вернулся из-за океана…

— …где блестяще распутали замысловатое преступление, — невозмутимо продолжил Холмсон.

— О да! — довольно улыбнулся Ватсон. — Думаю, даже вам моя история покажется любопытной.

— Надеюсь, — Холмсон пошуровал кочергой в камине и, устроившись в кресле, принялся набивать трубку.

— Недавно я побывал в Сан-Франциско, на конгрессе по судебной медицине, — начал свой рассказ Ватсон. — Провел там неделю и каждый день обедал в одном и том же ресторанчике, где собиралась занятная публика, наблюдать за которой — одно удовольствие для судебного врача и криминалиста. И вот однажды я стал свидетелем такой сценки.

Трое веселых парней решили развлечься на свой американский манер: к огромной колонне, около трех футов в диаметре, прилепили с помощью жевательной резинки серебряный доллар, вытащили свои кольты и начали соревноваться в меткости. А за колонной какая-то блондинка невозмутимо потягивала коктейль, любезничая с кавалером. Для парочки такие переделки были, видно, не в новинку, да и колонна укрывала надежно. Публика тоже не обращала внимания на пальбу, и мне пришлось делать вид, будто ничего особенного не происходит. Но тут блондинка за колонной вскрикнула и стала сползать под столик; ее светлое платье обагрилось кровью. Как из-под земли появились полицейские, схватили парней, а я поспешил на помощь пострадавшей. К счастью, она оказалась всего лишь в обмороке: пуля разбила ее бокал, содержимое которого и приняли сначала за кровь. А когда девица очнулась, выяснилось, что один из стрелявших парней — Том Найс — был отвергнутым ее поклонником.

— Простите, Ватсон, — Холмсон подложил полено в угасающий камин, — так в чем же, собственно, сложность этого… происшествия?

— Полиция совершенно растерялась, и если бы не я… Парни, что развлекались стрельбой, по их словам, знать не знали, кто находится за колонной. И напирали на то, что при всем желании не могли подстрелить эту пташку, даже рикошетом. И если бы не я, полиция отпустила бы с миром всю эту бандитскую компанию…

— И что же вы, дорогой Ватсон? — полюбопытствовал Холмсон.

— Дорогой профессор! — торжественно произнес Ватсон. — С тех пор, как вы показали мне, что физика может пригодиться в криминалистике, я добавил ее к моему арсеналу. При этом еще и получил массу удовольствия, знакомясь с ее историей… Тем более, что история физики не требует особых знаний математики… Да, так на чем я остановился? На том, что полицейские уже было собрались отпустить Тома Найса и его дружков, как вдруг я вспомнил о пятне Пуассона, что позволило предъявить задержанным обвинение в покушении на убийство!

— А где же, Ватсон, «удивительные совпадения»?

— Ну разве не удивительно то, что как раз накануне вечером я читал книгу по истории оптики, где, кроме прочего, рассказана история о пятне Пуассона?!

— Напомните, пожалуйста, и мне, — попросил знаменитый сыщик, — что это за пятно.

— Неужели вы не знаете?! — изумился Ватсон.

— Дорогой друг, — улыбнулся Холмсон, — вы уже не раз объясняли мне довольно простые вещи. Устраните же и этот пробел в моем образовании.

Ватсон прокашлялся:

— Когда в физике еще царила корпускулярная теория света, Френель выдвинул идею, что свет — это волны. Великий Пуассон, ознакомившись с этой работой, ехидно заметил: «Если дело обстоит так, как утверждает месье Френель, то в центре тени, которую отбрасывает на экран непрозрачный диск, должно быть светлое пятно. Абсурд!» Однако опыт провели, и… в центре тени нашли крохотное светлое пятнышко! Его-то и назвали пятном Пуассона.

— Занятно, — сказал Холмсон. — Не знал, что эта штука так называется. Но какое, собственно, отношение имеет эта история к той стрельбе?

Ватсон снисходительно улыбнулся:

— Дорогой профессор, согласно квантовой теории не только свет, но и любое тело обладает волновыми свойствами. Пули также подвластны эффекту Пуассона. И преступнику это было известно: он сознался, что читал научно-популярные книжки. Стреляя в колонну, Том Найс рассчитывал попасть в центр «тени» и прикончить блондинку, имея бесспорное алиби. Он не сомневался в научном невежестве полицейских. И это ему удалось бы, если бы не ваш покорный слуга…

— Браво, Ватсон. Однако, — вздохнул профессор, — вашей версии не хватает пары чисел.

— ???

— Пули, говорите вы, подвластны эффекту Пуассона? Но давайте прикинем, какова сила этой власти…

И после небольшой паузы профессор подытожил:

— Что-то вроде десяти в минус тридцать четвертой степени.

— Ради бога, профессор! — голос Ватсона дрогнул. — Что это значит?

— Это значит, что для осуществления предположенного замысла бравому парню понадобилось бы палить в колонну без отдыха на протяжение десяти… э-э-э… в двадцать седьмой степени лет. Другими словами, в миллиарды миллиардов раз дольше, чем существует наша Вселенная. Полагаю, что за это время он придумал бы что-нибудь поостроумней. Да и колонна рухнула бы за это время от усталости.

— Профессор, умоляю!.. Откуда эти миллиарды миллиардов?!

— Во-первых, дорогой Ватсон, еще Галилей понял, что книга природы написана на языке математики. Во-вторых, действительно, будь свет старинными корпускулами, тень от круглого предмета была бы идеально темным кругом. А согласно волновой теории эта идеальная тень «портится» из-за дифракции. Светло в тех местах экрана, куда световые волны, идущие по разным путям, приходят в фазе. Центр тени — как раз такое место. Но размер этого светлого пятнышка пропорционален длине волны. А для пули длина волны де Бройля — которую вы, вероятно, имели в виду — равна очень малой константе Планка, деленной на ощутимую величину массы пули и на ее большую скорость. Так что пятно Пуассона для пуль чрезвычайно мало, если даже забыть о некогерентности источника «пулевых волн». Соответственно мала и вероятность попадания пули в центр тени.

— Но… Пусть вероятность и мала, но всё же… не равна нулю! И ведь убийце могло повезти?! — отчаянно предположил Ватсон.

— Теоретически не исключено. Однако наша Вселенная слишком молода, чтобы обеспечить подобное везенье, — невозмутимо заметил Холмсон.

— А как же разбитый бокал? — не сдавался Ватсон.

— Холмсон неторопливо поднялся с кресла, положил трубку на каминную полку и снова взял в руки скрипку.

— Готов побиться об заклад, — улыбнулся он, — что среди посетителей ресторана была еще одна девица — скорей всего, брюнетка. И сгорала от ревности. А блондинка стояла на ее пути…

— Я понял! — воскликнул Ватсон. — Брюнетка, которой колонна не мешала, под шум чужой пальбы незаметно выстрелила в соперницу…

Вздохнув, профессор прижал подбородком скрипку.

— …но промахнулась и в суматохе скрылась, — воодушевленно продолжал Ватсон.

В ответ ему зазвучала прелюдия си-бемоль минор с ее переплетением двух тем. Ватсону почудилось, что это сама наука высоким чистым голосом воспевает свою историю, а та задает ей вопросы о прошлом и будущем…

Предел Бремермана, или cGh-криминалистика

— У научной криминалистики появился сильный соперник, — мрачно сказал Ватсон, входя в комнату, — научная преступность. Сегодня из статьи о квантовой теории информации понял, что беспредельная мощь науки несет миру опасностей не меньше, чем благодеяний.

— Да, я слышал, что у палки как правило два конца, — профессор Холмсон, похоже, был настроен скептически. — А о беспредельности неплохо сказал Эйнштейн: «Лишь две вещи беспредельны: Вселенная и человеческая глупость», — и оговорился, что не вполне уверен в первом.

— При всем почтении к Эйнштейну, в вопросах квантовой информации его мнение не столь существенно. Ведь он так и не принял квантовую теорию!

— Важнее то, что он сделал для ее создания. И что выяснил один из пределов науки — скорость света. Кстати, не первый предел в истории науки. Раньше обнаружили невозможность вечного двигателя, то бишь закон сохранения энергии. А затем и невозможность вечного двигателя второго рода, т. е. полного преобразования тепловой энергии в работу. Так что невозможность догнать и перегнать свет — это третье свидетельство мощи науки в обнаружении своих пределов.

— В физике компьютеров пределов не видно. Согласно закону Мура — Хауса скорость компьютера удваивается каждые полтора года. Квантовые же компьютеры наверняка ускорят темп прогресса. И в результате… у хакеров окажутся еще более мощные отмычки к секретным замкам Интернета.

— Закон Мура — Хауса?

— Как я понял из статьи, это не очень-то и закон, а наблюдение за развитием компьютерной техники, но наблюдение уже многолетнее.

— А в статье не сказано о пределе Бремермана?

— Никаких пределов. А что это и кто это? Физик?

— Вы не слышали про Бремермана, я не слышал про вашего Мура — Хауса. И это в век информации!

— Мур и Хаус — это два человека, основатель и сотрудник корпорации Intel, главного производителя компьютерных мозгов.

— А Бремерман — это один человек, но в трех лицах: математик, переключившись на биологию, свой самый знаменитый результат — упомянутый предел — получил, опираясь на физику. Если верить ему, никакая реальная система обработки информации не может делать более чем 10⁴⁷ операций в секунду на грамм массы системы. А 10⁴⁷ — это скорость света в квадрате, деленная на постоянную Планка: c2/h. Гигантская, кажется, величина. Но ничтожная по сравнению, скажем, с числом вариантов черно-белой мозаики в квадрате 20 × 20 элементов. Это более чем стозначное число, и чтобы перебрать все эти варианты, предельно быстрому компьютеру с массой, равной массе Земли, потребовалось бы время, гораздо большее возраста Вселенной.

— Математик стал биологом, а получил результат в физике?! И такой простой… комбинация из двух букв… Странно…

— Не менее странно, что ваша статья о компьютерах промолчала об этом пределе. Но, должен сказать, это не просто странность одной статьи. Впервые узнав о пределе Бремермана, я захотел уточнить, как эта простая формула получается, и обнаружил странный статус этого результата в научной литературе. Бремерман опубликовал его в начале 1960-х годов. Результат сразу же был принят одним из основоположников кибернетики — Эшби. Однако ныне, полвека спустя, предел Бремермана оказался в странном состоянии. Он присутствует в научных текстах разного уровня от солидных монографий до популярных статей и «Википедии», но и отсутствует в не менее солидных книгах и статьях. Отсутствует и в «Британской энциклопедии». При этом не удалось мне найти и сомнений в самом результате, не говоря уж об его опровержении.

— Для начала, профессор, объясните, пожалуйста, одну простую вещь. Если я правильно понимаю, информация — величина не физическая, а математическая. Когда какое-то сообщение кодируется или декодируется, речь идет о буквах и символах, но не о физических телах или их движениях. Так при чем же масса, скорость света и постоянная Планка?

— Заметьте, Ватсон, Бремерман говорил не о самой информации, а о ее обработке — точнее, о скорости этой обработки. Этот процесс происходит в какой-то материальной системе технического или биологического происхождения — в компьютере или в живом существе, которые подчиняются законам физики.

— …но также ведь и химии или нейрофизиологии?

— Конечно. А еще есть и свойства данной инженерной конструкции, если говорить о компьютере. Но Бремерман задался вопросом о максимально возможной скорости, ограниченной лишь самыми общими законами физики. Учет других законов и свойств компьютера может лишь уменьшить этот предел, если он, конечно, существует. Ведь законы химии и техники не нарушают законы физики.

— Логично. А неужели такая простая формула Бремермана — это результат длинных и сложных рассуждений?

— Вовсе нет. Можно сказать, в две строчки. Первая, самая знаменитая, формула физики

$$E=mc^2$$

согласно теории относительности, это максимальная энергия, какой может распоряжаться система массой m. А вторая строчка — формула квантовой теории, одно из соотношений неопределенностей:

$$\Delta t \cdot \Delta E > h.$$

Подставляя вместо ΔЕ максимальную энергию Е = mс², получаем минимальное время одной операции:

$$\Delta t_B=\frac{h}{mc^2}=10^{-47}\frac{1}{m},$$

если время выражено в секундах, а масса — в граммах. Обратная величина этого времени

$$\frac{1}{\Delta t_B}=\left(\frac{c^2}{h}\right)m=10^{47}m \ операций \ в \ секунду$$

и есть предельная скорость компьютера согласно Бремерману. Так что всё элементарно, дорогой Ватсон.

— Действительно… Если не считать соотношения неопределенностей.

— Вы хотите сказать, что равенство Е = mс² вам совершенно ясно?

— По крайней мере, как-то привычно.

— На эту тему имеется микрокомикс, где перед задумчивым Эйнштейном на доске написаны три формулы

$$E=mc, E=mc^2, E=mc^3$$

каждый образованный зритель недоумевает: «Чего он думает?! Ведь совершенно ясно, какая правильная».

— Тем удивительнее, что о пределе Бремермана молчит «Британника»! Есть ли у вас какое-то объяснение этому?

— Объяснения нет, но будь я во главе «Британники», я бы поместил статью о предельной скорости компьютера, где объяснил бы, почему изящная формула Бремермана… уязвима.

— Как?! Вы же только что воспроизвели его элементарно простой вывод?!

— Говорят, всё гениальное просто, но никто еще не сказал, что всё простое правильно.

Когда я впервые познакомился с пределом Бремермана, сделанным из двух фундаментальных констант, я спросил: «А где же третья?» Вы, Ватсон, полагаю, знаете, что в нынешней физике гравитационная константа G имеет столь же фундаментальный статус, как и скорость света с и постоянная Планка h. Все эти три константы — и только они — участвуют в теоретическом описании любого физического явления. И если иногда можно пренебречь какими-то из них, то лишь по соображениям практическим, когда не требуется высокая точность. Лишь эти три константы участвуют в формулировках самых общих на сегодняшний день физических теориях — теории относительности, квантовой теории и теории гравитации.

Поэтому я и заподозрил, что Бремерман недооценил константу G. Подозрения, разумеется, не достаточно. Если он ошибся, надо понять, где. И я, кажется, понял. Используя формулу Е = mс², он фактически привлек теорию относительности, в которой скорость света с максимальна. Но при этом охарактеризовал компьютер лишь одним параметром — массой m, — пренебрегая всеми другими, начиная с его характерного линейного размера L. На это он имел бы право, если бы рассматривал интервалы, много большие времени L/c, за которое свет пролетает расстояние L. В противном случае следует ограничить время одной операции Δt > L/c. Предельный компьютер делает свои компьютерные операции «всем своим телом» — иначе лишние части тела можно удалить. Значит, условие

$$\Delta t>\frac{L}{c}$$

следует добавить к квантовому условию

$$\Delta t>\frac{h}{\Delta E}$$

и следствию теории относительности

$$\Delta E<mc^2.$$

Эти три неравенства привели бы к пределу Бремермана

$$\Delta t>\Delta t_B=\frac{h}{mc^2},$$

если можно было бы выбирать L достаточно малой: L < h/(mc). Однако полной свободы в выборе величин L и m нет, поскольку существует гравитация, и здесь на сцену выходит третья универсальная константа — гравитационная константа G. Чтобы компьютер не превратился в черную дыру и не исчез за горизонтом событий, должно выполняться условие L > Gm/c². В результате получаем минимальное время операции:

$$\Delta t_{min}=\sqrt{\frac{Gh}{c^5}}\approx10^{-43} \ \mathrm{c},$$

или максимальное быстродействие компьютера:

$$\frac{1}{\Delta t_{min}}=10^{43} \ операций \ в \ секунду.$$

При этом Δt_min совпадает с известным квантово-гравитационным cGh-пределом ΔtcGh, за которым существующие физические теории не пригодны и требуется теория квантовой гравитации. Теорию эту ищут уже почти сто лет, начиная с самого Эйнштейна.

И обратите внимание, Ватсон, предел этот уже не зависит от массы компьютера. Так что никак не поможет увеличение этой массы до массы Земли. Единственное — и немаловажное — обстоятельство состоит в том, что создание квантовой теории гравитации может изменить физику непредсказуемым образом. И тогда придется заново рассмотреть вопрос о предельном быстродействии компьютера. Но в любом случае это будет не предел Бремермана².

— Теперь понятно, почему о нем умалчивает «Британская энциклопедия».

— Вряд ли поэтому, дорогой Ватсон. Иначе там написали бы о cGh-пределе, заодно воздав должное Бремерману за саму постановку вопроса. Ограничивают ли физические законы быстродействие любой системы последовательной обработки информации? Не только криминалисты знают, что задать хороший вопрос бывает важнее, чем дать на него ответ.

— Быть может, рано писать о квантовой гравитации, о которой ничего не известно? И, вероятно, саму величину cGh-предела невозможно объяснить простыми словами?

— Квантовой гравитации посвящено более сотни книг и многие тысячи статей, а величину cGh-предела можно объяснить школьнику.

— Тогда объясните, пожалуйста, и мне.

— Извольте. Сделаем мысленный физический прибор — две одинаковые массы m, связанные взаимным гравитационным притяжением, движущиеся по окружности и разделенные ее диаметром d. Астроном назвал бы это «двойной звездой», физик — «молекулой гравития». Подчинив эту систему классической механике и квантовому постулату Бора, выясним, при каких значениях параметров m и d теоретическое описание системы подойдет к границе своей применимости.

Ньютонов закон движения mа = F при подстановке в него центростремительного ускорения а = v²/r и силы тяготения F = Gm²/d² даст

$$\frac{mv^2}{r}=\frac{Gm^2}{d^2}.$$

Добавим к этому квантовый постулат Бора (с точностью до двойки и π)

$$mvr=nh.$$

Эта система из двух уравнений собственно и есть наш теоретический прибор. А его теория подойдет к границе своей применимости, когда скорость v приблизится к скорости света с, а целое число n примет наименьшее значение n = 1. Полагая в наших уравнениях v = с и n = 1, легко получить, что cGh-теория необходима при $d_{cGh}=\sqrt{Gh/c^3}\approx10^{-33}$ см, когда время одного оборота — уже знакомая вам cGh-величина $\sqrt{Gh/c^5}=10^{-43}$ с.

Ну разве это не элементарно, Ватсон?

— Действительно. Но как же тогда объяснить странное общественное положение всего этого вопроса?!

— А вот на этот вопрос у меня, дорогой Ватсон, ответа пока нет. Надеюсь на вашу помощь, — сказал профессор Холмсон и поднял скрипку, которую уже давно взял в руки.

Резкое стаккато Ватсон готов был назвать фугой XXI века, но признался себе, что в этой фуге не понимает ни фига.

Геннадий Горелик, канд. физ.-мат. наук, историк науки

¹ Впервые опубликовано в приложении к журналу «Квант» № 3 за 2013 год «Новые слова науки — от маятника Галилея до квантовой гравитации». М.: Изд-во МЦНМО, 2013 (Библиотечка «Квант». Вып.  127).

² Gorelik G. Bremermann’s Limit and cGh-physics. arxiv.org/abs/0910.3424v3