Скандал с кватернионами

В издательстве Corpus под эгидой «Книжных проектов Дмитрия Зимина» вышел перевод книги британского популяризатора науки Майкла Брукса (Michael Brooks) «Искусство большего: как математика создала цивилизацию» (“The Art of More: how mathematics created civilisation”). Автор защитил диссертацию по квантовой механике в Университете Сассекса, затем переквалифицировался в научного журналиста, публиковался в изданиях New Scientist, The Guardian, The Independent, The Observer, выпустил несколько научно-популярных книг и даже создал «Научную партию Великобритании». «Посвящая по главе различным подразделам математики — алгебре, геометрии, математическому анализу, статистике, теории информации, — Брукс нащупывает идеальный баланс между научной и популярной составляющими книги», — отмечает переводчик книги Заур Мамедьяров, канд. экон. наук, заведующий сектором экономики науки и инноваций ИМЭМО РАН. Мы публикуем отрывок из книги с любезного разрешения издательства.

Как i попало в Алису

Герой этой истории — ирландский математик. Уильям Роуэн Гамильтон родился в Дублине в 1805 году. Возможно, его биографы преувеличивают, но утверждается, что он был настолько смышлен, что к десяти годам успел освоить десять древних языков, включая халдейский, сирийский и санскрит. Но мальчик и правда был весьма одарен: когда в семнадцать лет он прочел недавно опубликованный трактат Лапласа о механике небесных тел, он нашел в нем ошибку, которую не заметил больше никто. Уже в двадцать два года он стал королевским астрономом Ирландии. К тридцати годам он был посвящен в рыцари за заслуги в развитии наук.

Это случилось в 1835 году, в тот же год, когда Гамильтон увлекся комплексными числами. Ему искренне хотелось продвинуться дальше в этой сфере. Он рассудил, что если чисто мнимое число i дает нам дополнительное измерение в пространстве чисел, то нельзя утверждать, что других измерений в этом пространстве нет. Он решил провести эксперимент и предложил два дополнительных набора чисел — по сути, два дополнительных измерения на числовой оси. Обозначив их j и k, он стал изучать, какие арифметические действия может с ними произвести, подобно тому, как Бомбелли поступил с квадратным корнем из –1 (ныне известным как i) тремя столетиями ранее.

Оказалось, что Гамильтон мог приписать j и k математические свойства, которые позволили бы ему осуществлять сложение и вычитание в «тройке» — так он называл совокупность i, j и k. А вот с умножением и делением ничего не выходило. Гамильтон был твердо настроен расширить набор допустимых операций, и это находило отражение в вопросе, с которым дети обращались к нему каждое утро. «Ну что же, папа, — говорили они, когда отец спускался к завтраку, — ты научился умножать тройки?» Гамильтон, по его же словам, отвечал им, «печально качая головой»¹.

А затем у него всё получилось. Его озарение стало предметом известного анекдота из истории математики. 16 октября 1843 года он прогуливался с женой вдоль дублинского канала Ройал и вдруг понял, в какой взаимосвязи должны состоять i, j и k, чтобы задача обрела решение. «В тот миг я почувствовал, как замыкается гальваническая цепь моей мысли, и искры, вылетевшие из нее, дали мне базовые уравнения, связывающие i, j и k», — вспоминал он. Он так обрадовался, что, боясь упустить свою мысль, выцарапал решение на камне ближайшего моста. Следы его вандализма давно исчезли, уничтоженные годами и прикосновениями. Сегодня место, где на Гамильтона снизошло озарение, отмечено табличкой, на которой высечено и выражение, сложившееся из отдельных искр:

i² = j² = k² = ijk = –1

Гамильтон добавил свою тройку к знакомому набору действительных чисел, чтобы создать то, что он назвал кватернионами. Он сказал, что создал это слово, опираясь на греческую идею о тетрактисе — изначальном мистическом наборе из четырех элементов. Эта связь была не случайной. Гамильтон полагал, что ученые сделаны из того же теста, что и древнегреческие мыслители. Он говорил, что им следует «изучать язык оракулов Вселенной и прислушиваться к ним»² . Он также разделял любовь греков к поэзии и близко дружил с поэтами-романтиками Вордсвортом и Кольриджем. По мнению Гамильтона, крайне важно было восстановить связь науки с философией и поиском божественного начала. И он считал, что кватернионы стали первым шагом в нужном направлении.

На следующий день после открытия Гамильтон написал своему другу Джону Грейвзу, который был юристом, но глубоко интересовался алгеброй. Грейвз ответил смело: зачем на этом останавливаться? «Я пока не понимаю, насколько мы вольны по своему усмотрению создавать мнимые числа и наделять их сверхъестественными свойствами», — отметил он в ответном письме 26 октября. Два месяца спустя Грейвз снова написал Гамильтону. Он снова удвоил число мнимых чисел и разработал математику октонионов. Словно бы в угоду музыкальным вкусам древних, двое ученых создали числовую октаву.

Они попытались пойти дальше, но у них ничего не вышло. Теперь мы знаем, что шансов у них не было, потому что сделать это невозможно. Складывается впечатление, что природа сложена из наборов чисел, но количество их конечно. Математики доказали это с октонионами, и мы получили полный комплект возможных систем, с помощью которых люди могут чрезвычайно эффективно описывать Вселенную на языке чисел.

Как же это происходит? Вас вряд ли удивит, что это сложно. Настолько сложно, что, похоже, легло в основу одной из величайших сцен англоязычной абсурдистской литературы: безумное чаепитие у Шляпника в «Алисе в Стране чудес».

Под псевдонимом Льюис Кэрролл скрывался оксфордский математик Чарльз Лютвидж Доджсон. Он преподавал геометрию в колледже Крайст-черч. По природе он был довольно консервативен, из книг больше всего любил «Начала» Евклида и похвалил чистую математику своего героя в книге “Curiosa Mathematica”: «Ее очарование, полагаю, заключается главным образом в абсолютной однозначности результатов, ведь именно этого больше всех сокровищ разума и жаждет человеческий интеллект. Нам лишь бы быть хоть в чем-то уверенными!» Можно смело сказать, что Доджсон не особо жаловал экспериментальные идеи и прогресс.

Его самое известное сочинение родилось в 1864 году и поначалу было довольно скучной рукописью под названием «Приключения Алисы под землей». В нем не было и намека на чаепитие. Но в ходе работы над ним Доджсон всё сильнее разочаровывался в том, как развивается его любимый предмет. Евклидова алгебра устаревала, ее сменяла абстрактная — в частности, комплексные числа и кватернионы. Доджсон писал о своих опасениях сестре, обсуждал их с коллегами и транслировал их в статьях для математических журналов, но казалось, что никто его не слушает. И тогда он применил один из любимых риторических приемов Евклида: доведение до абсурда. «Алиса в Стране чудес» полна насмешек Доджсона над математическими тенденциями, которые нравились ему меньше всего ³. Там есть выпады в сторону отрицательных чисел, символической алгебры и области, называемой проективной геометрией, и ее «принципа непрерывности» (чтобы высмеять ее идеи, Доджсон превратил младенца в свинью). Специалист по английской литературе Мелани Бэйли, собравшая из отдельных кусочков мозаики общую картину, полагает, что Доджсону наверняка доставляло особенное удовольствие проносить такие отсылки в дом Генри Лидделла, декана колледжа Крайст-черч⁴. Лидделл был отцом Алисы — той самой девочки, которая стала героиней первой истории Доджсона. Бэйли обнаружила документы, подтверждающие, что Доджсона сердило включение символической математики в оксфордскую учебную программу и что он лично повздорил об этом с деканом Лидделлом как раз в то время, когда писал «Алису». Бэйли представляет, как Доджсон включил свои аргументы в отредактированную версию книги, которую он передал семейству Лидделл, чтобы его возражения оказались на столе в гостиной декана как тайная шутка — или шутка, понятная лишь сторонникам Доджсона.

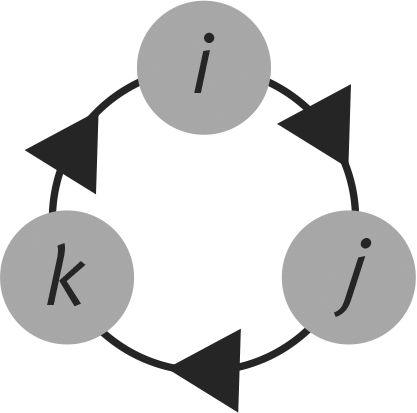
Несмотря на нелюбовь Доджсона к символической алгебре, именно кватернионы Гамильтона вдохновили его на самую яростную атаку. На чаепитии у Шляпника Алиса встречает трех странных персонажей: самого Шляпника, Мартовского Зайца и Соню. Алиса замечает, что герои постоянно пересаживаются. Похоже, это отсылка к одной из величайших инноваций Гамильтона — его способу умножать и делить кватернионы. Он схематично изображен на рисунке.

Дело в том, что в случае с кватернионами имеет значение порядок умножения. Мы говорим, что 2 × 3 равняется 3 × 2. Но i × j (или k) не равняется j × i (или — k). Важно, как именно вы двигаетесь по кругу. Разговор Алисы с Мартовским Зайцем — следствие недоверия Доджсона к новой математике: как отмечает Безумный Шляпник, «говорить то, что думаешь», — вовсе не то же самое, что «думать то, что говоришь». Тем временем четвертого героя — Времени — на чаепитии нет. Из-за его отсутствия возникает проблема: на часах всегда шесть — и всегда пора пить чай. Здесь Доджсон, похоже, отвечает на громкое заявление Гамильтона, что кватернионы тесно связаны с проблемой представления времени, существующей в физике. В 1835 году Гамильтон написал книгу «Алгебра как наука чистого времени». Изобретение кватернионов дало ему основание предположить, что одно из четырех чисел — время. В одном из своих (вполне берущих за душу) стихов Гамильтон отметил: «Один от Времени, три от Пространства — цепь символов должна закольцеваться». Он представлял время четвертым измерением, но время не идущее, а существующее, статичное и абсолютное, или, по его словам: «До и после; прошедшее, последующее и одновременное; непрерывное бесконечное течение из прошлого через настоящее к будущему». Оказывается, Гамильтон был склонен к философствованиям. «Есть нечто таинственное и запредельное в понятии Времени, — писал он, — но есть в нем также и нечто определенное и ясное, и если метафизики размышляют об одном, то математики строят свои рассуждения, отталкиваясь от другого». Это несколько многословнее некоторых цитат о времени другого его великого толкователя — Альберта Эйнштейна. Сразу вспоминается, как Эйнштейн сказал: «Единственная причина для существования времени — чтобы всё не случилось одновременно». Но это, по сути, всё та же мысль: время в голове — лишь иллюзия. И сцена из книги Доджсона показывает, что он этого не признавал: без Времени нет прогресса.

Своей теорией относительности это доказал Эйнштейн, а не Гамильтон. И для разработки специальной и общей теорий относительности, которые описывают свойства пространства и времени и поведение объектов при движении по ним, ему даже не понадобились четырехмерные кватернионы Гамильтона. В математике шла война, напоминающая войну видеоформатов Betamax и VHS. В конце концов кватернионы уступили инновационным векторам, которые определяют числа, указывая направление и расстояние на числовом эквиваленте навигационной карты. С тех пор кватернионы считаются жалким подобием векторов. Однако, хотя Эйнштейн и использовал четырехмерные векторы, мы по-прежнему можем смело благодарить Гамильтона за то, что он поместил идею о четвертом измерении в сердца и головы всех тех, кто хотел открыть доступ к космосу пифагорейцев. И хотя кватернионы очень мало используются в реальном мире, родственные им октонионы вполне могут стать ключом к финальной теории физики.

Восьмеричный путь

Даже Уильям Роуэн Гамильтон, неустанный поборник своих кватернионов, не стал продвигать октонионы. Четырехмерная алгебра позволяла учитывать время. Но какая польза от восьмимерной алгебры? Что делать с этим дополнительным пространством? Особенно коль скоро его математические законы столь запутанны.

Кватернионы состоят в довольно простой математической связи. Но когда Грейвз понял, что арифметические операции можно также производить в восьми измерениях, ему пришлось прокладывать новые — и, казалось бы, несуразные — пути. Например, положение скобок в выражении никогда прежде не имело значения. Но с октонионами 3 × (4 × 5) не было равно (3 × 4) × 5.

При работе с обычными числами математики начинают вычисления со скобок. Так, вычисляя произведение 3 × (4 × 5), они получили бы 3 × 20, или 60. Но если бы скобки переместились в другое место, ничего бы не изменилось. Вычисляя произведение (3 × 4) × 5, они получили бы 12 × 5, то есть тоже 60.

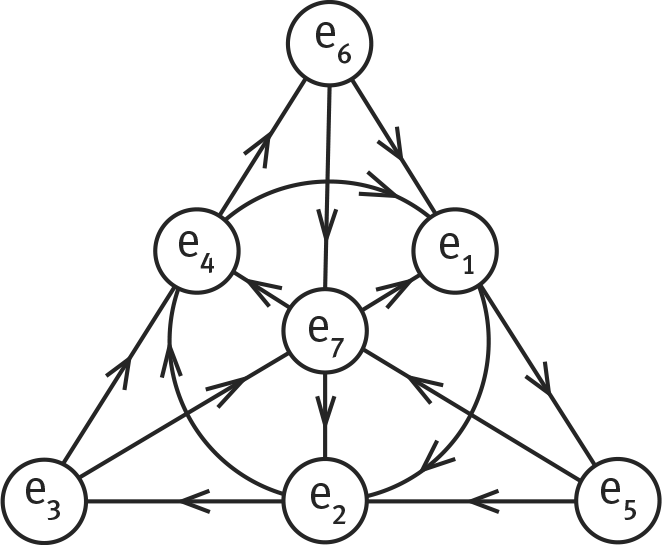
Но к октонионам обычные правила неприменимы. Если в кватернионах используются три числа i, j и k, то в октонионах их семь: e1, e2, e3, e4, e5, e6 и e7. Если хотите знать, e1, e2 и e4 сравнимы с кватернионами i, j и k. На рисунке показано, как они работают вместе в математических целях.

В некотором роде это прекрасно. Эта карта ландшафта октонионов называется плоскостью Фано в честь итальянского математика Джино Фано. В ней есть нечто мистическое, напоминающее о всевидящем оке, которое можно найти на обратной стороне Большой печати США и долларовой купюры. Математики эпохи Возрождения смотрели на него и видели око Бога, заключенное в треугольник, символизирующий христианскую Святую Троицу. Их современные коллеги — по крайней мере, некоторые — видят кое-что иное: краткое описание того, как устроена Вселенная.

Этот фрагмент математики пока не изменил историю человечества. Работа с октонионами еще не завершена, и она, возможно, ни к чему нас не приведет. Но эти странные числа дразнят нас, а их свойства отражают наши представления о поведении сил и частиц, которые встречаются в природе, и этого достаточно, чтобы некоторые физики отправились за ними вниз по кроличьей норе.

Мы уже упоминали о некоторых странных свойствах квантовой теории. Когда мы описываем поведение различных субатомных частиц, некоторая странность в получающейся математике отражает свойства кватернионов. Рассмотрим принцип неопределенности Гейзенберга. Он гласит, что нельзя одновременно точно знать определенные пары характеристик частицы — например, ее координаты и импульс. Это следствие того, что в квантовой математике порядок вещей имеет значение, как и при работе с кватернионами i, j и k.

Неразрешимая странность квантовой теории оттолкнула от нее и Эйнштейна, и Шрёдингера. Они вместе искали ее недостатки и пытались убедить остальных — в частности, Нильса Бора, который часто считается отцом-основателем квантовой теории, — что лучше начать всё с начала. В 1939 году Эйнштейн прочел лекцию, на которой присутствовал Бор. Глядя ему прямо в глаза, Эйнштейн заявил, что теперь его цель состоит в том, чтобы сместить с позиций квантовую механику⁵.

Шрёдингер также не стал дальше развивать квантовую теорию и отошел от нее примерно тогда же, когда и Эйнштейн. Оба ученых — независимо друг от друга — занялись разработкой теории, которая объединила бы квантовую физику с теорией относительности. Им хотелось создать грандиозную финальную теорию, которая включала бы в себя и описание космических свойств Вселенной из теории относительности, и объяснение субатомного мира и действующих в нем сил из квантовой теории. Так появилось бы единое математическое описание всего космоса. Ни один из двух ученых не преуспел в этом начинании, и они сильно разругались, публично критикуя труды друг друга⁶. После одного особенно колкого замечания о проблемах в рассуждениях Эйнштейна, сделанного Шрёдингером на пресс-конференции, Эйнштейн наказал бывшего друга и три мучительных (по крайней мере, для Шрёдингера) года не отвечал на его письма.

Теперь эстафету перехватили другие, но никто пока не заявил о близости к цели: математики и физики, а также все, кто работает в плодородных областях на стыке этих наук, по-прежнему исследуют различные пути. Любопытно — особенно в контексте этой главы, — что сегодня оптимизм в ученых вселяет в основном как раз математика комплексных чисел, в частности октонионов.

Всё началось с теории струн. Это попытка построить все частицы и силы физики, начав с довольно простой вещи — вибрирующих струн энергии. Струны вибрируют определенным образом — и мы получаем электрон. Вибрация другого типа дает нам электромагнитную силу. Идея о том, что математика музыки переплетена с математикой космоса, весьма заманчива: пифагорейцам она бы точно понравилась.

Но такой подход работает, только если мы допускаем существование «дополнительных» пространственных измерений (отличных от тех, что предложил Луи де Бройль). Согласно теории струн, к трем измерениям, в которых мы живем, нужно добавить еще семь скрытых. В этой схеме свойства вещества взаимодействуют друг с другом такими способами, которые математически описываются с помощью октонионов. Хотя теория струн вряд ли станет итогом наших размышлений, на текущий момент она, пожалуй, представляет собой лучшую из имеющихся у нас вариаций описания «квантовой теории гравитации» и подсказывает нам, что в финальной теории, какой бы она ни оказалась, вполне может фигурировать математика октонионов.

Эти подсказки проистекают из того, как специалисты по физике частиц собирают свой «зоопарк». Стандартная модель — это нечто вроде зоологической классификации, которая позволяет распределять частицы по классам на основании сходства их характеристик. Так, в класс адронов входят кварки, с которыми мы встречались в главе об алгебре. Адроны обладают электрическим зарядом, кратным заряду электрона (при этом множителем может быть и ноль). Вероятно, вы слышали о протонах и нейтронах, составляющих ядро атома. Это адроны. Существует и множество других классов, включая лептоны (к ним относятся электроны) и бозоны (например, бозон Хиггса).

Из-за различных классификаций, характеристик и особенностей поведения этих частиц Стандартная модель оказывается довольно запутанной. Нам сложно понять, как выводятся ее законы. Но есть основания предполагать, что запутанность возникает лишь потому, что мы пока не поняли, как модель соотносится со всеми тонкостями плоскости Фано и как в ней участвует гравитация. Лауреат Абелевской премии математик Майкл Атья отметил: «Настоящая теория, которую мы хотим вывести, должна сочетать гравитацию со всеми этими теориями так, чтобы гравитация казалась следствием октонионов… Это будет сложно, ведь мы знаем, что с октонионами не бывает легко, но такая теория, когда она будет обнаружена, окажется прекрасной и уникальной»⁷.

Но пока, разумеется, это лишь гипотетическая возможность для применения комплексных чисел. Но есть и другая прекрасная теория, чрезвычайно практичная и применяемая уже более века. Ее подарил нам Чарльз Протеус Штейнмец, родившийся в Германии. И именно эта история показывает нам — возможно, нагляднее любой другой, — в каком долгу наша цивилизация перед математикой.

¹ Baez J. The octonions. Bulletin of the American Mathematical Society. 39, no. 2 (2002): 145–205.

² Altmann S. L. Hamilton, Rodrigues, and the quaternion scandal. Mathematics Magazine. 62, no. 5 (1989): 291–308.

³ Bayley M. Alice’s adventures in algebra: Wonderland solved. New Scientist, 19 December 2009.

⁴ Мелани Бэйли, электронное письмо автору от 22 апреля 2020 года.

⁵ Isaacson W. Einstein: his life and universe. New York: Simon & Schuster, 2007.

⁶ Halpern P. Einstein’s Dice and Schrödinger’s Cat: how two great minds battled quantum randomness to create a unified theory of physics. New York: Basic Books, 2016.

⁷ Graduate Mathematics, Michael Atiyah, From Quantum Physics to Number Theory [2010], 2015, youtube.com/watch?v=zCCxOE44M_M.