Даниэль Канеман и теория перспектив

27 марта 2024 года в возрасте 90 лет скончался Даниэль Канеман, лауреат премии по экономике памяти Альфреда Нобеля 2002 года, заслуженный профессор Принстонского университета и один из основателей поведенческой экономики. О том, что же важного внес в науку Даниэль Канеман, рассказывает Егор Бронников (Университет Маастрихта, Европейский университет в Санкт-Петербурге).

Ко второй половине XX века в среде стандартных академических экономистов стало господствующим достаточно специфичное представление о людях, принимающих решения, как о максимально рациональных агентах, нацеленных на максимизацию своей полезности — т. е. меру удовлетворения от нахождения в определенном состоянии мира — и не совершающих систематических ошибок (что отчасти было связано с простотой моделирования, отчасти — с нормативными утверждениями теории, а отчасти — с философской традицией). Несмотря на присутствующие к этому времени (и продолжающие появляться) эмпирические свидетельства, противоречащие стандартной теории (в первую очередь парадокс Алле), большинство экономистов относилось к ним скептически, оставаясь под влиянием парадигмы стандартной рациональности агентов.

С появлением поведенческой экономики, зарождение и развитие которой в огромной степени связано с именами Даниэля Канемана, Амоса Тверски и Ричарда Талера (вместе с большим количеством экономических психологов), фокус экономических исследований в значительной степени сместился в сторону описания человеческого поведения с сохранением методологической строгости определения факторов, которые на него влияют. Будучи смежной областью экономики и психологии, поведенческая экономика занимается изучением разнообразных (в первую очередь не сугубо денежных) факторов принятия решений.

Одной из важнейших работ в поведенческой экономике стала (и остается до сих пор) статья Даниэля Канемана и его главного соавтора Амоса Тверски под названием «Теория перспектив»¹, расширяющая обычное понимание того, как люди принимают решения в условиях риска. В то время, как стандартная теория предполагала, что агенты имеют устойчивые и непротиворечивые предпочтения, работа Канемана и Тверски продемонстрировала несколько ключевых отклонений.

Теория ожидаемой полезности

Начнем с рассмотрения лотереи G_A = [x₁, p₁; . . . ; x_I, p_I], где x_i — это денежный исход, а p_i — вероятность наступления этого исхода. Поскольку это довольно общее представление будущих исходов, оно часто используется при моделировании принятия решений ².

Стандартная теория ожидаемой полезности предписывает индивидам преобразовывать денежный выигрыш x_i специальным образом, используя функцию полезности (⋅), и взвешивать каждый из этих преобразованных результатов на основе объективной вероятности p_i. Сумма каждого члена подобного правила составляет ожидаемую полезность игры (см. формулу $\eqref{eq1}$), которую, согласно стандартной теории ожидаемой полезности, рациональный агент должен максимизировать.

$$\pmb{E}U(G_{A})=\pmb{E}U(x_i)=\sum_{i}p_ix_i \tag{1}\label{eq1}$$

Согласно теории ожидаемой полезности, агент может быть либо склонным к риску, либо нейтральным к риску, либо избегающим риск. Все эти три концепции относятся к выборам, которые индивиды совершают, отдавая предпочтение лотереям или гарантированным выигрышам. Лица, склонные к избеганию риска, предпочли бы гарантированный выигрыш лотерее. Степень их избегания риска отражается премией за риск, т. е. суммой, которую они готовы заплатить, чтобы избежать участия в лотерее. Хотя теория ожидаемой полезности определяет, какими должны быть предпочтения агента к риску, она предписывает рациональным агентам иметь неизменные предпочтения к риску.

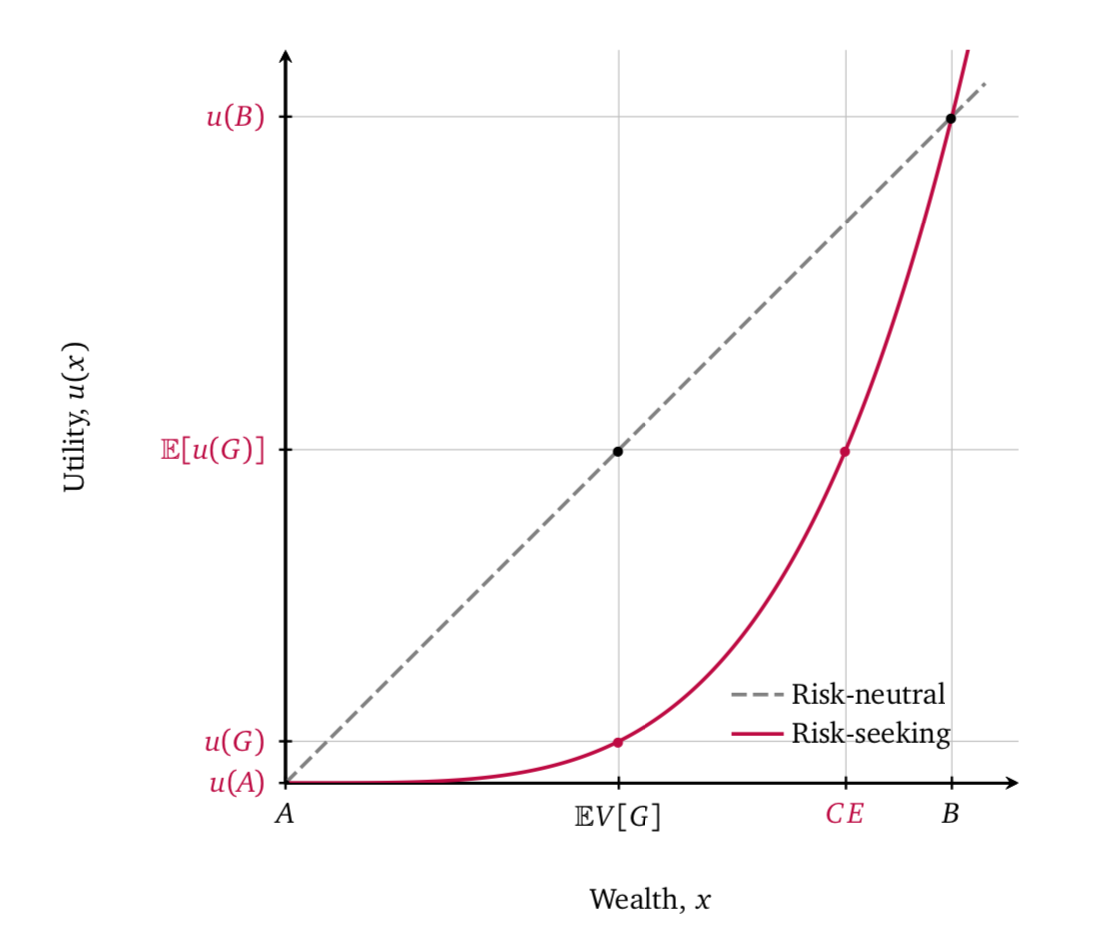
Для более наглядного объяснения рассмотрим случай агента, склонного к риску (что отражено на рис. 1). Предположим, есть лотерея G = [, ; , ]. Ожидаемая стоимость этой лотереи составляет () = ⋅ +  ⋅ . Это дает два важных значения с точки зрения теории ожидаемой полезности: (()) = () и () = (). То есть разница между эквивалентом определенности и ожидаемой полезностью лотереи G — это денежная сумма, которую человек готов заплатить, чтобы иметь возможность принять участие в лотерее, а не получить что-то определенное (то есть отрицательная премия за риск).

Теория перспектив

В отличие от теории ожидаемой полезности, теория перспектив описывает другое преобразование денежного выигрыша x_i (с помощью функции ценности (x_i)), а также дополнительное преобразование (объективной) вероятности p_i (с помощью функции взвешивания вероятностей (p_i)).

Теория перспектив включает несколько ключевых элементов, которых нет в теории ожидаемой полезности: (i) взвешивание вероятностей, (ii) эффект перехода, (iii) избегание убытков и (iv) зависимость от точек отсчета.

Учитывая эмпирические доказательства того, что в среднем люди имеют тенденцию завышать небольшие вероятности и занижать высокие вероятности, теория перспектив моделирует этот феномен с помощью нелинейной функции взвешивания вероятностей (что выражено формулой $\eqref{eq2}$ и показано на рис. 2).

$$\pi_i(p_i)=\frac{p_i^{\gamma}}{\left[p_i^{\gamma} + (1-p_i)^{\gamma} \right]^{\frac{1}{\gamma}}} \tag{2}\label{eq2}$$

Функция ценности преобразует результаты, учитывая предпочтения, которые в среднем проявляют люди в своем отношении к риску, зависящие от того, находятся ли они в области выигрышей или убытков (см. формулу $\eqref{eq3}$ и рис. 3). Конечная оценка значения лотереи, в соответствие с теорией перспектив, выражается суммированием оцененных перспектив, взвешенных по вероятностям, и дает значение перспективы или игры (см. формулу $\eqref{eq4}$).

$$\begin{equation}\tag{3}\label{eq3}
v{(x_i)} =
\begin{cases}
x^{\alpha} &, x \geqslant 0 \\
-\lambda(-x)^{\beta} &, x<0
\end{cases}
\end{equation}$$

$$\pmb{V}(G_{A})=\pmb{V}(x_i, p_i)=\sum_{i}\pi_i(p_i)v(x_i) \tag{4}\label{eq4}$$

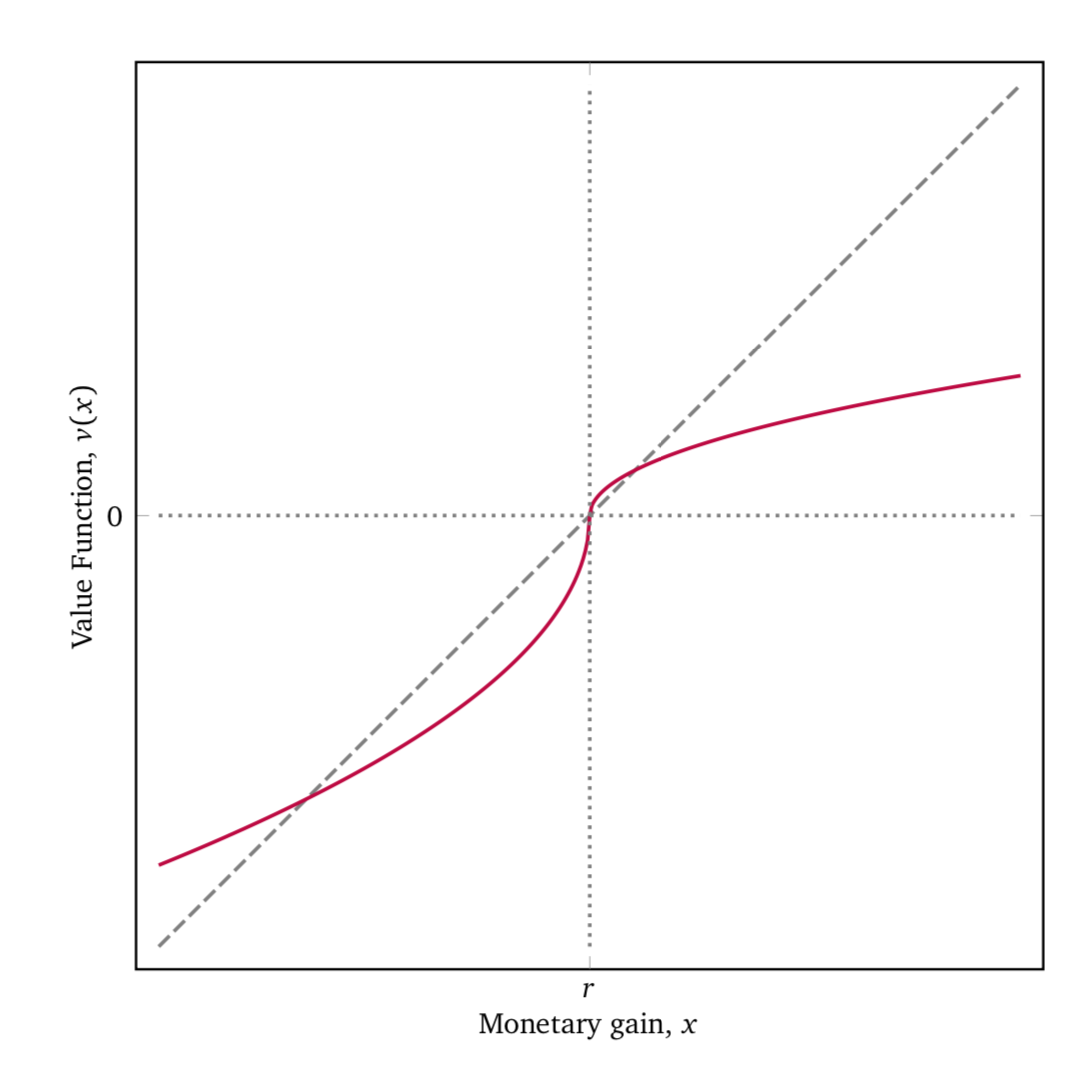
Экспериментальные данные показывают, что люди ведут себя как те, кто склонен избегать риска, когда перед ними стоит выбор между возможностью получить большой выигрыш, но со сравнительно небольшой вероятностью, и получением значительно меньшего выигрыша, но гарантированного. Однако как только выбор предлагается между потерей существенной суммы со сравнительно небольшой вероятностью и потерей небольшой суммы гарантированно, люди в среднем предпочитают первое (то есть ведут себя как стремящиеся к риску). Этот феномен известен как эффект перехода, т. е. изменение предпочтений к риску как только пересекается точка отсчета.

Впоследствии теория перспектив, оказавшаяся самой цитируемой работой для авторов и одной из самых цитируемых статей, когда-либо опубликованных в одном из самых престижных экономических журналов Econometrica, нашла широкое применение в разных областях экономики, финансах и общественной политике. По совокупности всех работ Даниэль Канеман получил мировую славу и признание классиком, запечатленное, к примеру, в почетной ежегодной лекции его имени Международной ассоциации исследований в экономической психологии (IAREP) и в названии Центра поведенческих наук и государственной политики при Принстонском университете (совместно с Энн Трисман).

---

¹ Kahneman D., Tversky A. Prospect Theory: An Analysis of Decision under Risk // Econometrica. 1979. Vol. XVLII. P. 263—291.

² В качестве иллюстрации можно рассмотреть следующую игру. Если при броске (математически правильной) монеты выпадает орел, то тот, кто согласился участвовать, получает 5 долларов, а если выпадает решка — участник должен заплатить 5 долларов. Тогда эта игра будет представлена следующей ставкой: G = [–$5, 1/2; $5, 1/2].