Давайте не будем говорить о политике и политиках, а поговорим о выборах просто как о процедуре подсчета голосов. Поэтому постараемся обойтись без фамилий и названий партий – будем, если надо, говорить просто о победителе.
Нам важно понять, можем ли мы отличить случаи, когда при подсчетах голосов (бюллетеней) происходит постороннее вмешательство (попросту мухлёж), от случаев честного счета. И, если сможем отличить, то удастся ли оценить масштаб вмешательства прямо «в голосах». Исходными данными для нас будут официальные цифры Центризбиркома РФ, которые он запрятал очень глубоко, разбив на тысячи фрагментов и представив их не в самом удобном виде, но простим ЦИКу эту маленькую хитрость – закон они соблюли, данные есть, и эти данные умеют говорить не только то, что запланировал ЦИК.
Если говорить о федеральных выборах, то для анализа мы имеем протоколы почти 100 тысяч участковых избирательных комиссий (УИКов) с десятками чисел в каждом – а это большой статистический массив. Большинство этих чисел трех- или четырехзначные: например число избирателей или число действительных бюллетеней и т.д. Последняя цифра каждого такого числа должна быть любой от 0 до 9 – и можно ожидать, что все варианты тут примерно равновероятны.
Представьте себе, что вы взяли 100 телефонных номеров своих знакомых и смотрите, сколько из них кончается на 0, на 1, на 2…..на 9. Скорее всего, их будет примерно поровну – сильные отклонения без какой-то причины (скажем, политики телефонной станции, которая распределяет номера каким-то особым образом,или желания иметь «круглый номер», или, наконец, вашего желания иметь знакомых, телефоны которых оканчиваются каким-то особым образом) будут удивительны. Конечно, не следует ожидать, что их будет по 10 каждого типа – какая-нибудь последовательность типа (9, 12, 8, 13, 6, 11, 10, 8, 9, 14) вас вряд ли так уж удивит, ведь возможны случайные отклонения.
Вы, наверняка удивились бы, если бы ноль встретился все 100 раз и ни разу не встретилась бы другая цифра. Если вам кто-то скажет, что у него получилось именно так, то вы наверняка заподозрите подвох, а попросту обман. И вы будете правы: вероятность такого исхода – это единица, деленная на единицу с сотней нулей!
В теории вероятностей разработаны разные методы оценки того, какие отклонения правдоподобны, а какие нет. Мы не будем вдаваться в теорию этого вопроса, скажем только,что одним из употребительных критериев считается «хи-квадрат» и связанная с ним вероятность. Чем меньше эта вероятность, тем менее правдоподобна гипотеза о том, что в данных нет каких-то систематических отклонений. «Идеальное» значение вероятности по этому критерию 0,5 (50%), а много меньшие (или большие) значения вызывают подозрения. Если вероятность, скажем, 0,001, то это уже подозрительно: случайная выборка будет приводить к такому (или меньшему) значению лишь в одном случае из 1000.
Этот критерий можно применить к данным с выборов (в любой стране). И вот оказывается, что с числами ЦИК происходит странное: равномерность сильно нарушается, и значение вероятности того, что такая аномалия случайна, становится подозрительно низкой. Нули и пятерки в конце чисел встречаются подозрительно, неправдоподобно часто. А если брать две последних цифры, то особенно часто встречаются комбинации «00» и «50», даже в числе проголосовавших на дому.
Наименьших значений вероятности такого случайного события достигают на федеральных выборах 2008-го и 2011 года (60 и 30 нулей после единицы в знаменателе). В 2012 году значения повысились, но остались в «подозрительной» зоне – 25 нулей. Это число уже можно уместить в одну строчку: 1/10000000000000000000000000. Думаю, никто не удивится, что из всех регионов наиболее выдающиеся результаты показывает Дагестан (в нем дело доходит до 200 нулей), а из регионов с преимущественно русским населением – Кемеровская область.
Если смотреть последние цифры сразу в пяти графах протоколов (списочный состав, число выданных и действительных бюллетеней и число голосов за победителя выборов и занявшего второе место), то вот так развивались события по годам (график 1).
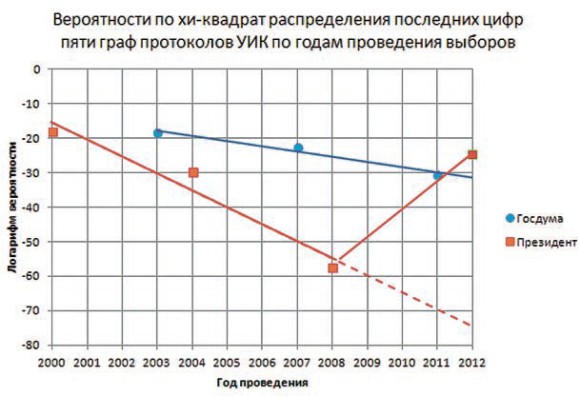 График 1. Федеральные выборы в РФ 2000-2012 годы
График 1. Федеральные выборы в РФ 2000-2012 годы
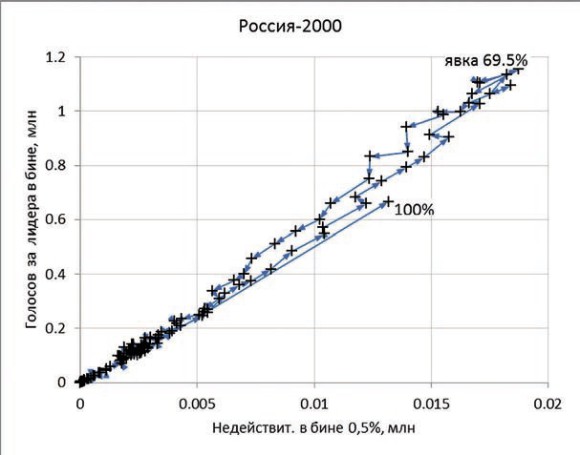
График 2. Президентские выборы в РФ 2000 года
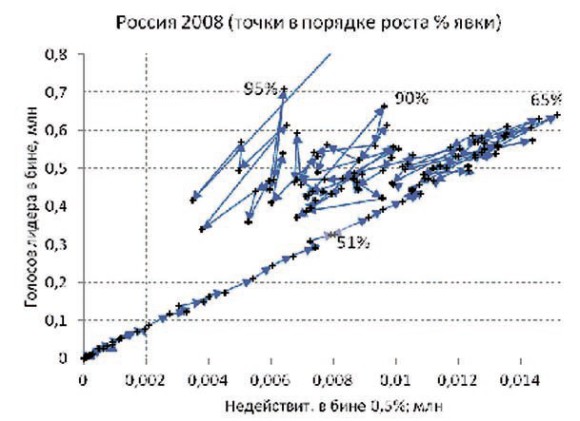
График 3. Президентские выборы в РФ 2008 года
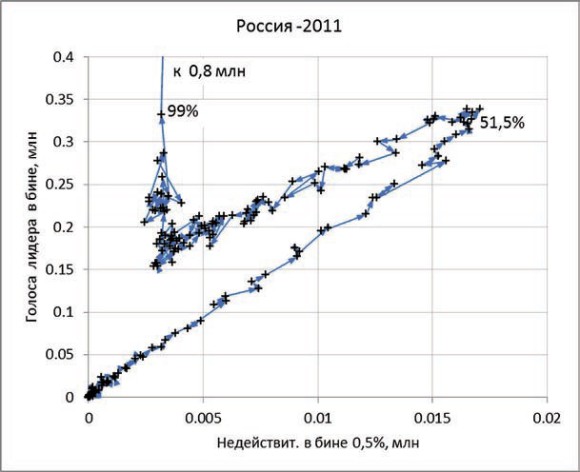
График 4. Выборы в госдуму 2011 года
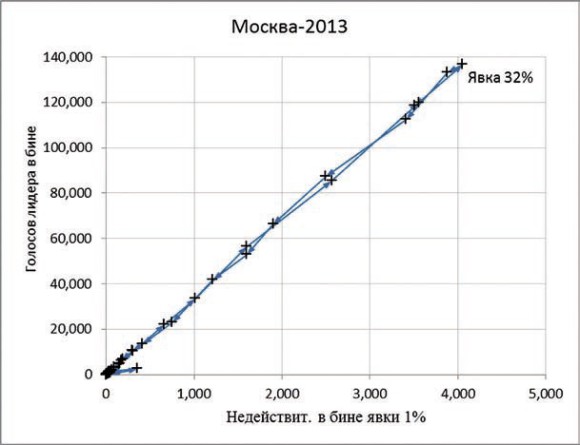
График 5. Выборы мэра Москвы 2013 года
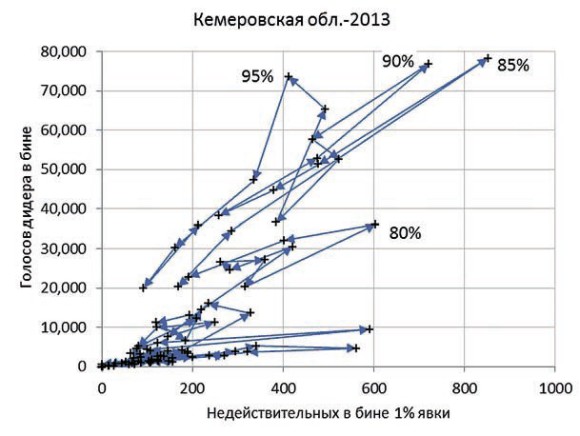
График 6. Парламентские выборы в Кемеровской области 2013 года
Видно, какую роль сыграли веб-камеры, установленные на участках, сломав идущую вниз красную прямую.
А что в других странах? Увы, там всё выглядит нормально: ниже 10% вероятность не опускается ни в Швеции, ни во Франции, ни в Польше, ни (даже!) на Украине или в Мексике (исключение – Уганда).
Но, может быть, дело в какой-то неучтенной мелочи? Можно проверить и это. Достаточно вспомнить, что последняя цифра числа – это остаток от деления на 10. Можно взять остаток от деления на 7 или 11 – и равномерность немедленно восстанавливается, а вероятности составляют десятки процентов! Ведь те, кто подгоняет цифры к требуемому результату, про остаток от деления на 7 не думают, а вот «круглые» десятичные цифры их тянут неотвратимо.
Можно проверить существование мухлежа на выборах и другим способом. Представим себе, просто предположим, что кто-то приписывает голоса с целью завысить явку и результат симпатичного ему кандидата или партии. Тогда он будет увеличивать число выданных бюллетеней, число действительных бюллетеней и число бюллетеней «ЗА» своего кандидата. Но вот число недействительных бюллетеней останется прежним: их увеличивать не хочется. Как это можно увидеть в масштабах России или ее отдельного региона?
Для этого можно объединить все УИКи в группы с примерно одинаковым процентом явки. Скажем, через 1% (или 0,5%, или даже через 0,1%). Таких групп будет 100 (или 200, или 1000). Для каждой такой группы подсчитаем общее число голосов «ЗА» за лидера и число недействительных бюллетеней. Построим график для президентских выборов 2000 года, который покажет наглядно, как связаны эти величины и как они изменяются в зависимости от явки.
Как видно из графика 2, чем больше число голосов «ЗА», тем больше и число недействительных бюлле-тений. Самые большие числа там, где наиболее распространенная явка (69,5%). Все точки примерно лежат на одной прямой, потому что на каждый недействительный бюллетень приходится примерно постоянное (около 59) число голосов «ЗА» при всех явках. Такую же картину можно увидеть, например, для Франции.
Но это если подсчет был честный. А если нет? Если приписывали голоса «ЗА»? Тогда появятся точки, в которых число голосов «ЗА» окажется намного больше ожидаемого при данном числе недействительных бюллетеней. Такая тенденция как раз наблюдается при анализе президентских выборов 2008 года.
При больших, более 65%, явках график 3 теряет какие-либо следы закономерного поведения, а последняя точка при 100% даже не умещается на графике – 1,4 млн голосов за лидера при 0,014 млн недействительных бюллетеней.
Но если это так, то тогда можно просто просуммировать все такие «лишние» голоса, точки которых расположились выше прямой линии при данном числе недействительных бюллетеней. Например, для точки при 95% явки вместо более 0,7 млн голосов останется менее 0,25 млн – почти полмиллиона голосов лишние. Или наоборот, можно подсчитать только ту часть голосов «ЗА», которые не «убежали» слишком высоко вверх от разумной прямой. Получается, что из 50 с лишним миллионов голосов победителя выборов ему приписано около 13 млн и оставить надо лишь менее 40 млн.
Посмотрим на выборы в действующую Госдуму (график 4). Здесь такая же оценка дает, что из 32 млн голосов лидеру выборов добавили более 10 млн.
Только что прошли местные выборы. В Москве, с ее тысячами наблюдателей, в 2013 году такие же графики ведут себя так, как им и положено.
Но выборы проходили и в регионах. Вот так выглядят результаты выборов в местный парламент в Кемеровской области.
Здесь, чтобы увидеть линейный участок вблизи начала координат, надо очень внимательно присмотреться. А на вопрос, сколько же из 1,5 млн голосов, полученных победителем, ему просто приписали, придется ответить, что более 1 млн.
Остается еще один, но главный вопрос: почему такие проверки не делает ЦИК со своим немаленьким аппаратом, получающим немаленькую зарплату от налогоплательщиков? Почему он спокойно принимает «на веру» явно нелепые цифры, которые ему присылают?
Но вопрос этот риторический и политический, а мы ведь условились о политике не говорить и не называть имен и партий.
Независимый эксперт С.В.
См. предыдущую статью С.В. «Про арифметику и немножко про выборы». ТрВ-Наука, 13 марта 2012 года, № 99, стр. 10-11. http://trv-science.ru/2012/03/13/pro-arifmetiku-i-nemnozhko-pro-vybory/

вообщето насколько я помню, не настаиваю конечно, при исследовании статистическом астрономических таблиц, помоему еще в 19в, было открыто что вероятность появления монотонн убывает : т.е. наиболее часто встречается 0 и 1 и реже всего 9. я не помню как это явление называется, но надеюсь более осведомленные читатели поправят меня.
Только в астрономии речь шла о первой цифре, а не о последней.
да это существенная особенность. но я так и непонял и не понимаю, почему такая ассимметрия 1х и последних чисел в этих измерениях. их по идее к какому базису ни приводи, все одно должно быть равномерное расперделение. может спустя века базы данных наполнились и все выровнялось?
Распределение первых цифр принципиально отличается от распределения последних.
Попробуйте посмотреть любой степенной ряд вида k^n. Единиц в начале будет почти всегда больше чем других цифр.
Поищите обоснование закона Бенфорда (Benford’s law).