- Аномалии в официальной статистике мартовских выборов подробно проанализировал Сергей Шпилькин в прошлом номере ТрВ-Наука [1]. О методологических основаниях их выявления и о значении этих аномалий для оценки результатов выборов рассуждает канд. биол. наук, доцент Департамента социологии Высшей школы экономики в Санкт-Петербурге Алексей Куприянов. Для интернет-версии статьи было добавлено три рисунка и пояснения к ним (см. ниже).
В связи с прошедшими выборами вновь оживились дискуссии об аномалиях в показателях электоральной статистики. В отличие от 2011–2012 годов, основной площадкой для обсуждения стал не «Живой Журнал», а «Фейсбук», однако некоторые темы оказались на удивление живучими. В частности, снова немало копий было сломано в ходе эпического противостояния «Гаусса» и «Чурова». Казалось бы, всё отспорено и решено, но до сих пор находятся как те, кто считает, что явка должна быть распределена нормально, так и те, кто полагает все оценки относительно фальсификации результатов выборов неверными на том основании, что явка вовсе не обязана следовать нормальному распределению. Благодаря упорству спорщиков мы еще долго не придем к согласию, но какой-то промежуточный итог подвести можно.
Почему распределение явки не должно быть нормальным?
Помимо социологических соображений о естественной пространственной сегрегации населения на это есть две чисто математические причины. Во-первых, область возможных значений явки — рациональные числа (т. е., числа, которые могут быть получены делением друг на друга целых чисел) в пределах от нуля до единицы, в то время как нормальное распределение непрерывно и бесконечно. Во-вторых, избирательные участки — это не случайные выборки из генеральной совокупности избирателей, и распределение средних показателей активности избирателей по ним (явок на участках) не может рассматриваться как случай, сводимый к Центральной предельной теореме1.
Распределение явок имело бы шансы приблизиться к нормальному, если бы участки формировали путем лотереи, проводимой среди всего населения страны (и несколько сотен счастливцев, вытянувших, скажем, номер 1768, где бы они ни жили, считались бы приписанными к участку с этим номером, точно так же как и вытянувшие остальные номера от 1 до 97 с лишним тысяч). Дело пошло бы еще лучше, если бы избиратели могли голосовать не целиком, а частями, отдавая, например, не 1, а любое случайное количество голоса от 0 до 1 (например, 0,967). Однако оба этих предложения довольно далеки от реальности.
Кроме умозрительных соображений есть сравнительные данные по разным странам [2]. Ни в одной из них распределение явки по участкам не проходит стандартных тестов на нормальность. Не всякое распределение с колоколообразным графиком плотности можно признать нормальным в строгом математическом смысле. Требуется не просто «колокол», а «колокол» вполне определенных пропорций. Гистограмма явки обычно более островершинна, чем плотность нормального распределения с теми же математическим ожиданием и дисперсией, и несколько асимметрична.
Каким оно должно быть в России?
Мы не знаем наверняка. Имеющиеся искажения весьма значительны. Где-то истинные распределения не угадываются вообще (например, Чеченская или Кабардино-Балкарская республики), где-то видны только их следы (Татарстан, Кемеровская область). Вместе с тем у нас есть определенные теоретические соображения о том, как формируется распределение явки. Избиратели принимают решение об участии или неучастии в голосовании под влиянием множества факторов, модифицирующих даже самые стабильные паттерны электорального поведения.
В результате каждый регион характеризуется своими средними показателями активности избирателей с определенным разбросом значений на участках, связанным отчасти со случайными факторами. Практически в каждом крупном регионе распределение явок должно быть приблизительно колоколообразным, слегка асимметричным (обычно из-за несколько более высокой явки и большего разброса значений на небольших «сельских» участках, чем на более крупных «городских»), с низкими «плечами»/«хвостами».
Регионы могут отличаться друг от друга средними значениями явки или показателями разброса, однако эти различия должны формировать какой-то разумный географический паттерн: Север против Юга, Запад против Востока, город против сельских поселений. Очень помогает наличие исторических «внутренних» границ (например, части Польши, ранее входившие в состав Российской империи, Пруссии и Австрии, бывшие ГДР и ФРГ в составе объединенной Германии, Север и Юг Италии или США). Эти паттерны относительно стабильны во времени и не могут резко и разнонаправленно изменяться от одного электорального цикла к другому.
Россия велика и разнообразна, но естественная гетерогенность ее населения не может объяснить ни того уровня различий, который наблюдается в характере распределений явки в разных регионах (например, почти нулевой разброс в Кабардино-Балкарии, Ингушетии и Чечне в отдельные годы против вполне «человеческих» показателей Свердловской области, Карелии или Хакасии), ни географических странностей — непонятно, почему сходный характер распределений показывают отдаленные друг от друга Татарстан, Краснодарский край и Кемеровская область, между и рядом с которыми расположены почти «идеальные» в плане электоральных показателей регионы вроде Свердловской или Новосибирской областей. Гипотеза о естественной гетерогенности не позволяет объяснить и радикальные изменения характера распределения явки в Москве между выборами в Думу в 2011 году и президентскими в 2012 году.
Почему оно не может совпадать с «распределением Чурова»?
Потому что аномалии не сводятся к асимметрии распределения явок. Одна из важнейших особенностей «распределения Чурова» — аномальное тяготение к круглым числам. Начиная приблизительно с 80% явки (а в некоторые годы и с более низких значений) такие выбросы расположены на каждом целом процентном пункте. В совместной статье Дмитрия Кобака, Сергея Шпилькина и Максима Пшеничникова [3] был предложен алгоритм оценки вероятности формирования таких выбросов, основанный на симуляции распределения явки. Их алгоритм генерирует диапазон вероятных значений не для «истинного» распределения явки, которое было и остается неизвестным, а для «распределения Чурова», исходя из предположения, что резкая асимметрия его, возможно, соответствует реальности.
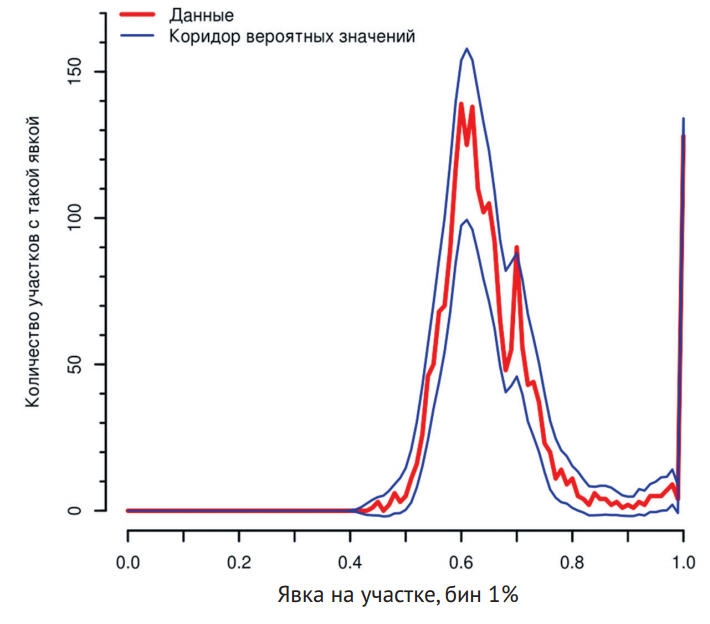
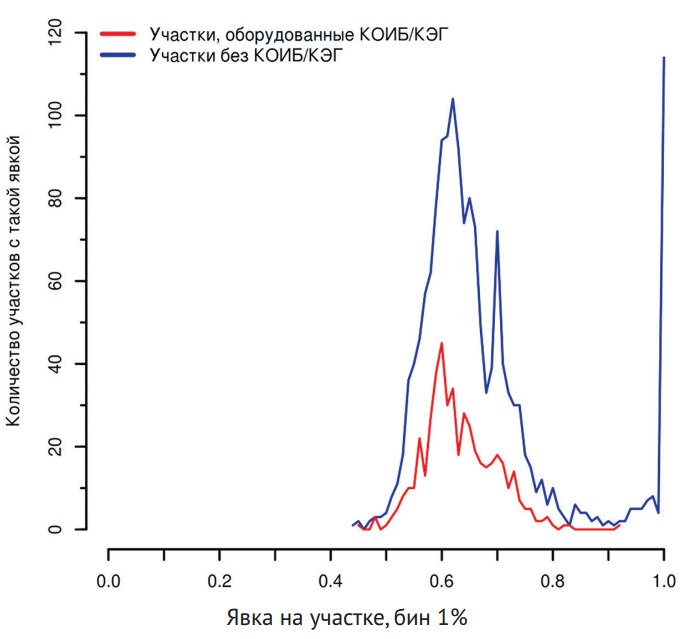
Анализ, вникнуть в логику которого и воспроизвести который может каждый желающий, показывает, что вероятность появления таких пиков в ходе естественных стохастических процессов ничтожно мала2. Этот метод, при всем его щадящем подходе к фальсификациям, достаточно чувствителен, чтобы зафиксировать аномальный характер явки даже в относительно «чистом» Петербурге (cм. рис. 1, 2). Этот метод позволяет надежно отличить естественные пики, обусловленные наличием «популярных» простых кратных отношений (1/2, 2/3, 3/4 и т.п.), от аномальных пиков, обусловленных «человеческим фактором».
К круглым числам тяготеют и исходные абсолютные показатели (например, количество действительных бюллетеней). Анализ частот последних цифр также показывает статистически значимые отклонения от ожидаемого равномерного распределения [4, 5].
Доказывают ли аномалии в электоральной статистике наличие фальсификаций?
Да. В предыдущем разделе я постарался объяснить, почему для этого достаточно математических соображений. Однако у нас есть не только они. За прошедшие годы накопились сообщения наблюдателей о вбросах бюллетеней и грубых нарушениях на этапе подсчета голосов, о расхождениях между цифрами в полученных наблюдателями копиях протоколов и цифрами в ГАС «Выборы».
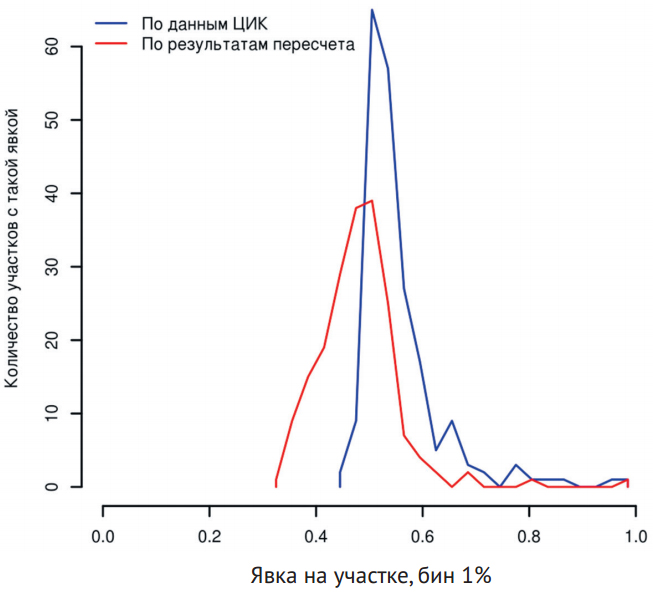
Eсть данные пересчета явки по официальным видеозаписям, значительно расходящиеся с данными, предоставленными участковыми комиссиями (рис. 3). В этом году работа c видеозаписями только началась, но уже первые результаты показывают на отдельных участках приписки в объеме от трети до двух третей голосов.
Все эти наблюдаемые манипуляции должны оставлять цифровые следы. Вбросы бюллетеней, «карусели» и подобные им технологии одновременно повышают явку и долю голосов за кандидата-бенефициара фальсификации, в результате чего облако точек на диаграмме рассеяния в осях явка/ доля голосов «размазывается» по дуге вверх и вправо, образуя хвост «кометы Чурова», сопровождающий ядро «честных» участков. Переброс голосов от одного кандидата к другому (без изменения явки) дает второе облако точек над основным ядром.
Согласованные действия фальсификаторов, ориентирующихся на определенный процент (часто некруглый) приводят к формированию полосовидных сгущений точек в неожиданных местах, вроде десятков участков с результатом «Единой России» в 62,2% на думских выборах в Саратове в 2016 году или 58% явки на губернаторских выборах в Петербурге в 2014-м.
Несогласованные действия тысяч фальсификаторов, ориентирующихся для простоты расчетов на целые или круглые проценты, приводят к формированию характерных пиков на целочисленных значениях в области высокой явки и высокой поддержки лидера (см. рис. 4). Они же отвечают и за избыточные частоты нулей в последних цифрах исходных показателей (например, числа действительных бюллетеней). Ту же природу имеет и «стена» в распределении явки на 50% в 2004 году, когда еще требовался кворум.
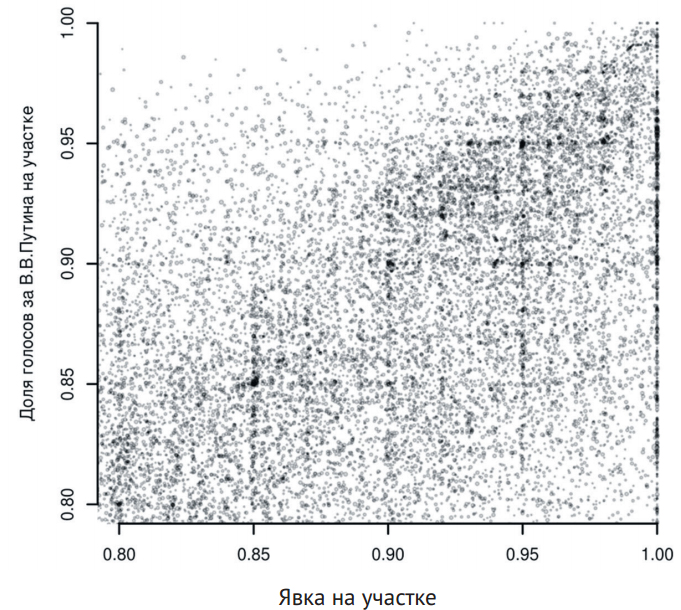
Осторожность требует говорить лишь о том, что наличие цифрового следа фальсификаций указывает на необходимость проверки. Однако проверки (например, пересчет явки по видео) только подтверждают наши осторожные подозрения. Сторонники альтернативных гипотез (пространственная сегрегация по социально-экономическим параметрам, совпадающая с границами избирательных участков, характер «мобилизации» избирателей в ходе избирательной кампании) пока не могут предъявить никаких сопоставимых по обоснованности результатов, которые помогли бы объяснить имеющийся масштаб аномалий.
Можно ли оценить масштабы фальсификаций и восстановить истинную картину явки?
Имеющиеся оценки носят приблизительный характер и, судя по всему, занижают масштаб фальсификаций. Связано это с тем, что в алгоритмы, на основе которых производятся вычисления, сознательно заложен ряд допущений «в пользу» фальсификаторов. Например, в модель Монте-Карло симуляции гистограммы явки, предложенной Кобаком, Пшеничниковым и Шпилькиным, заложено предположение о том, что явка на участках действительно такова, как в данных, предоставляемых ЦИК (что, как мы знаем, заведомо неверно).
Алгоритм для расчета превышения ожидаемой доли голосов тоньше — он отталкивается от того, что при «вбросе» бюллетеней одновременно с ростом явки должна расти доля только одного из кандидатов. При этом, во-первых, вынужденно не учитываются манипуляции в пользу других кандидатов (которые тоже иногда встречаются). Во-вторых, он нечувствителен к «перебросу» голосов от одного кандидата к другому. Наконец, не вполне ясно, насколько хорошо этот алгоритм работает в регионах с полностью или почти полностью нарисованными данными (в виду отсутствия базы для сравнения в виде пула «честных» участков), а таких регионов немало.
Неутомимый Сергей Шпилькин и другие энтузиасты обработали данные с детализацией до участков по всем президентским выборам начиная с 2000 года, пользуясь умеренной открытостью ЦИК. Если внимательно проанализировать эти данные, отсеивая все очевидные аномалии, остается всего несколько регионов с относительно стабильной репутацией: Алтайский край, Архангельская, Владимирская, Ивановская, Костромская, Магаданская, Мурманская, Сахалинская, Свердловская и Ярославская области, Ненецкий автономный округ, Республики Карелия и Хакасия.
Внимательный анализ показывает, что и они несвободны от аномалий (в частности, на выборах-2018 заметна незначительная аномалия явки в районе 70%), но на фоне других выглядят пристойно. (Есть еще около полутора десятков регионов, в которых в 2012 и 2018 годах аномалии носили весьма умеренный характер, например Москва; однако ситуация в предшествующие годы делает их непригодными для лонгитюдного (долгосрочного. — Ред.) анализа.)
Гистограмма явки, построенная по этим регионам, получается именно такой, как я описал выше: слегка асимметричной, с низкими «плечами», более островершинной, чем нормальное распределение с аналогичными параметрами (рис. 5). В ней даже есть пик на 100%. Есть основания полагать, что по России в целом всё должно выглядеть приблизительно так же.

Общее замечание о значении выявленных аномалий
Нередко приходится слышать, что выявляемые приписки не изменяют принципиально исход выборов или что они малы, поскольку доля участков, вносящих вклад, скажем, в аномальные пики на целых значениях процентов, ничтожна.
Мне представляется, что в обоих случаях это не так. Пики на правом «плече» распределения явки указывают не на точечные фальсификации на конкретных процентах, а на то, что, судя по всему, все в целом данные в области значений явки, превышающей 80%, не имеют почти никакого отношения к реальному волеизъявлению избирателей.
Наличие масштабных фальсификаций, охватывающих порой целые регионы, должно означать отмену результатов голосования на десятках тысяч участков, а возможно, и признание выборов в целом несостоявшимися. То, что этого не происходит, многое говорит нам о политической системе современной России.
Дополнительные материалы для Интернет-версии статьи.
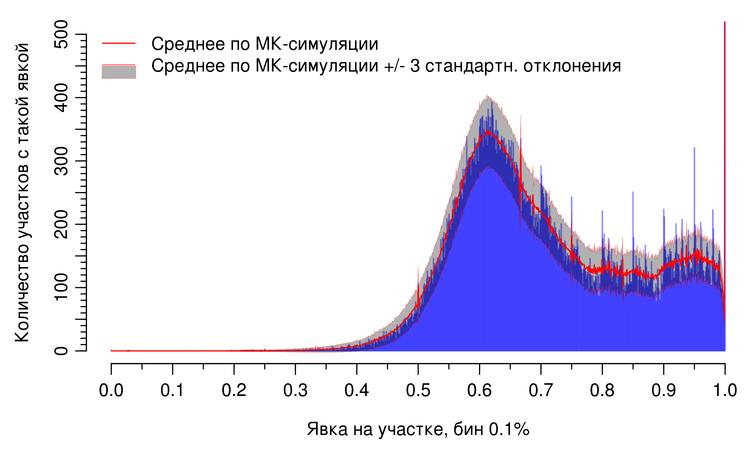
На этом рисунке представлены аномалии явки по России в целом во время президентских выборов 2018 года, гистограмма явки и коридор вероятных значений для гистограммы явки (среднее +/- 3 стандартных отклонения Монте-Карло симуляции). Обратите внимание на пики на кратных 5 и 10 процентах явки, выступающие далеко за пределы коридора и меньшего размера пики на каждом целом процентном пункте при явке выше 80%.
На этом графике (рис. 6) хорошо заметно отличие естественных пиков, связанных с часто встречающимися простыми кратными отношениями (например, 1/2 и 2/3, на 50% и 66,7% соответственно), и аномальными пиками. Над естественными пиками коридор вероятных значений так же образует узкий пик (включая участки со 100% явкой).
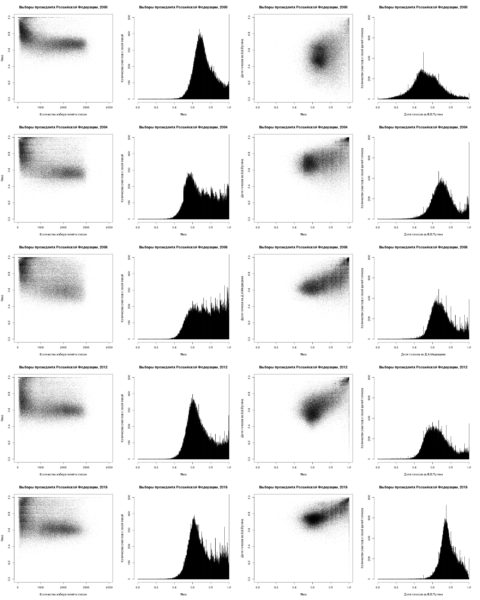
На Рис. 7 представлены диагностические графики для президентских выборов в России за 2000-2018 гг. Сверху – вниз: годы 2000, 2004, 2008, 2012, 2018. Слева – направо: диаграмма рассеяния в осях «количество зарегистрированных избирателей» / «явка на участке»; гистограмма явки на участках; диаграмма рассеяния в осях «явка на участке» / «доля голосов за лидера на участке»; гистограмма долей голосов за лидера на участке.
Обратите внимание на «волны» явки на «круглых» процентах, которые становятся заметны с 2004 году (в 2004 году особенно хорошо видна «волна» на отметке 50% — в этом году еще сохранялось требование о наличии квроума) и аналогичные «волны» доли голосов, отданных за лидера, наиболее заметные в 2008 году, но наблюдаемые с 2004 года. Заметно улучшение ситуации с явкой в 2012 году и ухудшение в 2018 году.
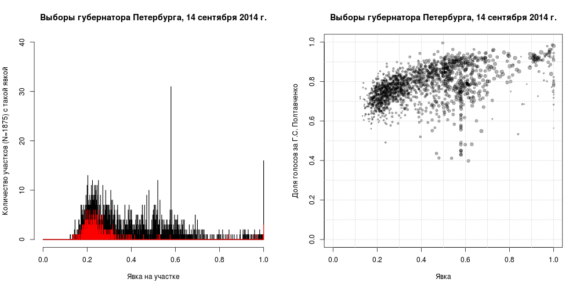
На рис. 8 представлены графики, отражающие аномалии явки на выбора губернатора Петербурга в 2014 году. Обратите внимание на вытянутое по дуге облако точек на диаграмме рассеяния справа и пик на 58% явки на обоих рисунках (31 участок с практически идентичными показателями явки). На гистограмме красным выделено распределение явок по участкам, подведомственным пяти территориальным избирательным комиссиям, в пределах которых не наблюдалось значительных аномалий (одно «ядро», нет «хвоста кометы»).
Благодарности
Я признателен Ефиму Галицкому [6], Роману Удоту и Дмитрию Рогозину за актуализацию дискуссий о форме распределения явки, Сергею Шпилькину за дополнительные пояснения по алгоритму симуляции, Борису Овчинникову [7] и Андрею Мятлеву за суммирование важных соображений в ходе дискуссии (их влияние заметно в этой заметке).
Алексей Куприянов
Графики построены автором на основе открытых данных.
1. Шпилькин Сергей. Выборы 2018 года: фактор X и «пила Чурова» // ТрВ–Наука № 252 от 24 апреля 2018.
2. Шалаев Н. Е. Распределение явки: норма и аномалии // Социодинамика. 2016. (7): 49–66.
3. Kobak D., S. Shpilkin, & Pshenichnikov M. S. Integer percentages as electoral falsification fingerprints // The Annals of Applied Statistics. 2016. 10(1). P. 54–73.
4. С. В. Голая школьная математика // ТрВ Онлайн, 28 февраля 2012.
5. С. В. Про арифметику и немножко про выборы // ТрВ Онлайн, 13 марта 2012.
6. Дискуссия, инициированная Ефимом Галицким.
7. Реплика Бориса Овчинникова.
1 Центральная предельная теорема — общее название ряда предельных теорем теории вероятностей, в которых устанавливается, что при большом числе слагаемых распределения сумм независимых случайных величин близки к нормальному распределению. — Ред. См.: Центральная предельная теорема // Большая российская энциклопедия.
2 Скрипт для обработки данных в среде R выложен на GitHub.

По поводу Рисунка 5: накладывать Гауссиану на распределение, ориентируясь на стандартное отклонение распределения, бессмысленно. Распределение явно сложено из разных частей, только одна из которых – Гауссиана. Если уж накладывать – нужно взять только первую часть распределения (до 70 с небольшим процентов явки) и наложить Гауссиану или Экспоненциально модифицированную гауссиану на этот участок. Заодно вычитанием можно будет прикинуть разницу. С аппроксимацией ЭМГ могу помочь.
Оно, разумеется сложено из разных частей (из которых, к тому же, ни одна не описывается нормальным распределением в свою очередь). Собственно, почти вся статья о том, что распределение явок по участкам не нормально, но это не значит, что фальсификаций нет.
А почему не смесью бета-распределений, не обделённой физическим смыслом?
Алексей, чему равна средняя явка для зелёного полигона частот с рис. 1 Шпилькина из предыдущего номера ТрВ и для синей плотности с Вашего рис. 5?
У Сергея Шпилькина график строится иначе: он считает не частоту участков с данным показателем явки, а количество голосов в данном бине явки. Грубо говоря, у меня по оси Y — кол-во участков с такой явкой, у него — количество людей, проголосовавших на участках с такой явкой. Они строятся на одних и тех же данных, дополняя друг друга.
1. Спасибо, Алексей, я это знаю. И даже различаю три метрологии, как тут
http://newsland.com/community/8232/content/kak-preumnozhit-sredniuiu-zarplatu-aktivnost-andronov-i-iavku-na-vybory/6322670
в такой шпаргалке
http://newsland.com/static/u/article_image/18/05/01/tmpN95Wl_.jpeg
В рамках которых у конструкторов сплайнов (полигонов частот) остаётся свобода. Тот же Джон Кислинг узлами сплайна, сочинённого по 100-разрядной гистограмме, выбрал бы не круглые проценты, а середины интервалов явки…
2. В Nature Reports etc. принято прилагать к статье файлы или адреса исходных данных. Намедни я обрадовался, обнаружив, будто “Голос” выложил в экселевском формате результаты 55 тыс. выборов, собранные с миру по нитке.
https://www.golosinfo.org/ru/articles/280
К сожалению, архив оказался нечитабельным.
В сети гуляет уйма графиков и оценок, полученных по предварительным и “окончательным” протоколам ЦИК о выборах 2018.
Вам не трудно выложить – для своих и для чужих студентов – не перегруженную лишними деталями таблицу официальных результатов выборов 2018? Или это уже кто-то сделал?
3. У меня сложидось впечатление, что С.А. Шпилькин, конфисковав (у правых столбиков гистограммы – на язык полигонов не буду переводить) заштрихованные голоса, не доводит конфискацию до уровня субъектов федерации, ТИК и (или) УИК, входящих в столбики. Точно так же он, похоже, поступает и при конфискации “лишних” голосов по местным гистограммам субъектов РФ. Думаю, что при таком подходе “федеральный вброс” может изрядно отличаться от суммарного “местного вброса”. Назло закону Ломоносова о сохранении вброшенной материи.
1. Сергей Шпилькин решает вполне определенную задачу — ему надо рассчитать абсолютный размер вбросов и оценить, какой вклад вносят участки с разной явкой (потому что методика вычисления вброса опирается на разность трендов изменения долей голосов за разных кандидатов при высоких явках). Т. е., тут вопрос не в манипуляции данными ради манипуляции данными, а в том, что эти графики показывают содержательно разные эффекты.
2. У нас тут пока не Nature Reports (жаль, конечно, но). Данные по 2018 г., которые использовал я (файл pres.2018.txt.zip), можно скачать здесь: https://github.com/alexei-kouprianov/Breaking-the-ice-with-R
3. Это интересное соображение, надо спросить у Сергея.
1. Спасибо, Алексей. Поразгадываю на досуге кухню разведки выборов.
2. Что-то все дружно Чурова стали вспоминать. Вот и Андрей Бузин скоро сделает доклад “Распределение Чурова”, говорит Программа этой конференции на странице 14.
http://soc-phys.ipu.ru/sites/default/files/Программа%20конференции%20online.pdf
Жаль, нельзя заглянуть в тезисы.
Кто вхож на конференцию ИПУ?!
Завтра (23-го) А. Бузин делает доклад по этим тезисам.
http://soc-phys.ipu.ru/system/files/10826.pdf
Моя “сырая” средняя явка по участкам = 0.7167, медианное значение явки по участкам = 0.6825. С графиком Шпилькина сложнее — там надо написать скрипт для преобразования данных (что я не смогу сделать раньше, чем вечером) и смысл получившейся метрики физически будет не вполне тривиален, хотя мы ее, конечно, получить можем.
Отклонение от гауссианы доказывает только одно: распределение не гауссово.
Почему оно не гауссово – вопрос отдельный. Может, фальсификация, но это не единственная возможность. В природе уйма негауссовых распределений.
Два математика сидят в баре, смотрят в окно. Выпили пива и решили поспорить. Один говорит:
– я спорю, что мимо окна пройдут 100 мужчин подряд и ни одной женщины!
Второй отвечает
– по гауссу, вероятность такого события 1/2^100 !!!
Первый говорит.
– ок. Я ставлю 100 фунтов.
И кто выиграл?
Мимо бара промаршировала рота солдат.
Фальсификация?
Или просто негауссово распределение?
Все это очень остроумно, но как объяснить сетчатый паттерн на рис. 4 без привлечения гипотезы о фальсификации результатов, я не знаю. И, в общем, никто не знает.
ну не знаю конечно. сеточка такая забавная.
но если взять отдельные районы где-нибудь на кавказе, то уже достижение, что там избирательные урны стоят 8-)))
а уж если туда в эту урну кто чего положил – то это вообще!
ну так. по ощущениям. народ-то дикий.
Не в Кавказе дело, а регионах, исторически унифицированных со времён Ивана Грозного.
ну что, история такая русского народа. не столько самим плодиться, сколько ассимилировать другие народности
“…история такая русского народа…”
Не в этом дело.
Дело в том, что там результаты голосования такие, как если бы никакого Ивана Грозного и всех последующих деятелей вообще не было.
“Отклонение от гауссианы доказывает только одно: распределение не гауссово.”
Там дело не столько в том, что оно не является гауссовым, сколько в том, что оно радикально отличается для разных регионов и разных выборов в одном и том же регионе.
Причём разница такая, как если на местах от выборов к выборам полностью менялось население.
И всё-то мы знаем о честных выборах…
http://maxpark.com/static/u/article_image/18/05/21/tmpouDIpD.jpeg
В графе Seats последней таблички первое 2011 читать как 2015.
А искали ли в этих данных распределение Парето и фрактальность?
Парето отыскалось!!! Особенно при явках больше единицы, то есть ста процентов.
Премодерацию наверняка не пройдёт но попробую: г. Нижневартовск , крупная нефтяная компания с иностранным капиталом. На утренней планёрке строится весь рук. состав спривлечением телеконференц связи начальникам дается указание обеспечить 100 % явку и политпропаганду типа мы всё равно узнаем кто за кого отдаст голос. Единовременно по всей стране проводятся аналогичные мероприятия в бюджетных организациях. Всё это вызывает у меня лютый фейспалм. Особенно радует “за открепительным пришёл , в прошлый раз мы за тебя голос отдали , и немнго нецензурного” всё в присутствии полиции наблюдаюшей за порядком, к слову наблюдателям выкатили на позапрошлых выборах по 17 тр. Я был “послан лесом” хоть без рукоприкладства. навсех плошадках аналогичная ситуация. Как-то так. Профит. А вы зачем-то статмод привлекли :)
Алексей,
Приведите пожалуйста подтверждение(ссылки на источники) ключевого тезиса в выводе, явно влияющего на смысл статьи.
Вы привели лишь одну ссылку на “Ассоциацию наблюдателей Татарстана”.
И, по одному приводимому вами случаю вы делаете обобщённый вывод обо всём процессе выборов во всей стране? Это случайная логическая ошибка?