
В воспоминаниях Виталия Лазаревича Гинзбурга о Ландау описана любопытная квалификационная шкала ученых «по достижениям», составленная Львом Давидовичем в молодые годы. В ней использовались десятичные логарифмы — т. е. считалось, что физик класса 1 сделал в 10 раз больше физика класса 2 и т. д.
«В этой шкале из физиков нашего века только Эйнштейн имел наивысший класс 0,5. Бор, Гейзенберг, Шрёдингер, Дирак и некоторые другие имели класс 1, а себя Ландау относил сначала только к классу 2,5, а потом перевел в класс 2 и, кажется, наконец, в класс 1,5. К классу 1 был отнесен и де Бройль, что вызывало некоторые возражения, но Ландау был тверд — наивысшее достижение де Бройля, пусть оно и не было подкреплено его дальнейшей деятельностью, действительно очень велико (речь идет о волнах материи. — Прим. В. Гинзбурга)» [1, с. 144].
Представитель древней аристократической фамилии Луи де Бройль стал, как и его старший брат Морис, физиком, но, в отличие от него, не экспериментатором, а теоретиком. Морис был ученым серетарем Первого Сольвеевского конгресса, проходившего в 1911 году в Брюсселе, и готовил к изданию его труды. Главной темой конгресса было обсуждение квантовой гипотезы Макса Планка. Морис пересказывал младшему брату выступления участников конгресса — лучших физиков того времени, показывал тексты их докладов. Эти рассказы пробудили у Луи интерес к физике атома. Впоследствии он вспоминал:
«Со страстностью, свойственной молодости, я увлекся обсуждавшимися проблемами и решил посвятить все свои силы выяснению истинной природы таинственных квантов, глубокий смысл которых еще мало кто понимал» [2, с. 347].
В 1924 году Луи де Бройль защищал в Сорбонне докторскую диссертацию «Исследования по теории квантов», где обосновывалась очень смелая гипотеза: каждую движущуюся материальную частицу можно рассматривать как волну, так называемую волну материи. Отсюда следовало, что в потоке электронов, например, можно наблюдать чисто волновые явления, такие как дифракция и интерференция. В то время это была лишь гипотеза. Соответствующие эксперименты были проведены три года спустя и полностью подтвердили предположение де Бройля.

Работа де Бройля не вызвала большого интереса среди физиков: ее результаты были чересчур умозрительными. Правда, Альберт Эйнштейн, которому его друг Поль Ланжевен послал копию диссертационной работы де Бройля, воспринял ее восторженно: «Он приподнял угол великого занавеса» [3, с. 265].
По-настоящему оценить научный прорыв де Бройля его коллеги смогли только после появления революционных статей Эрвина Шрёдингера, открывшего так называемую волновую механику.
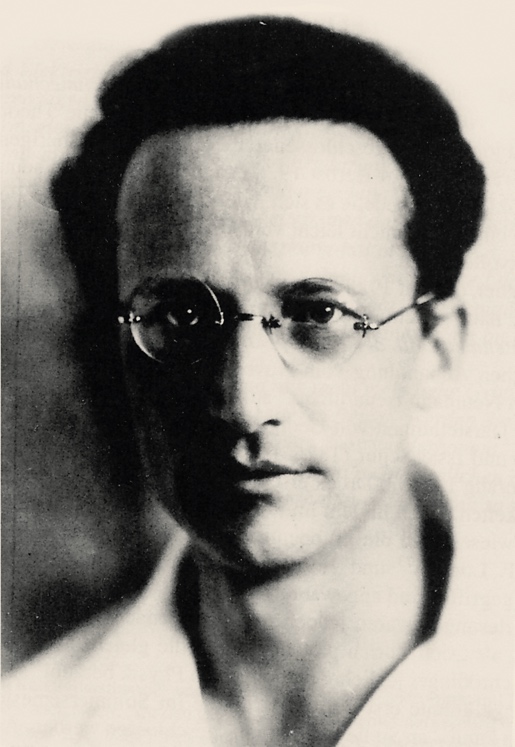
Тем самым к Гёттингену, Копенгагену, Кембриджу и Гамбургу, где создавалась новая квантовая физика, добавился швейцарский Цюрих. В этом городе в начале 1920-х годов собрались сильные физики и математики: в университете работал родившийся в Вене Эрвин Шрёдингер, а в более известном Политехникуме, где учился Альберт Эйнштейн, преподавали, например, Петер Дебай и Герман Вейль. Отношения между учеными сложились дружеские, если не сказать большего; атмосфера благоприятствовала творческому поиску и научному сотрудничеству. Коллеги часто проводили совместные коллоквиумы для студентов университета и Политехникума.
Феликс Блох, впоследствии первый докторант Вернера Гейзенберга, в то время изучал физику в цюрихском Политехникуме. Позже он вспоминал, как на одном из таких заседаний осенью 1925 года профессор Политехникума Петер Дебай обратился к коллеге из университета с предложением:
«Шрёдингер, в данный момент вы не заняты никакой важной прблемой. Не могли бы вы доложить нам о докторской работе де Бройля, которая привлекла к себе определенное внимание?» [4, с. 241].
Уже на следующем заседании коллоквиума Шрёдингер выступил с «чудесным и ясным сообщением», как выразился Феликс Блох, о работе Луи де Бройля. Докладчик особо выделил один результат работы: если допустить, что в стационарную орбиту электрона, движущегося вокруг ядра, длина волны, связанной с этим электроном, укладывается целое число раз, то квантовые условия Нильса Бора, введенные как постулаты, получаются автоматически. Далее произошло следующее:
«Когда докладчик закончил, Дебай заметил между прочим, что это преставление выглядит всё же по-детски. Как ученик Зоммерфельда, выступавший должен был бы знать, что для подходящего описания волны нужно иметь волновое уравнение. Это звучало довольно тривиально и не произвело большого впечатления, но Шрёдингер, очевидно, задумался над этой идеей более тщательно. Через несколько недель он снова выступил на коллоквиуме и начал такими словами: „Мой коллега Дебай порекомендовал использовать волновое уравнение. Ладно, я нашел его“. И далее он рассказал, по сути дела, то, что можно считать первым из исследований, опубликованных в Annalen der Physik под названием „Квантование как задача о собственных значениях“» [4, с. 241].
Фактически на глазах Феликса Блоха всего через несколько месяцев после создания «Работы трех» рождалась «волновая механика», ставшая мощным конкурентом и соперником «матричной механики». Создатель нового подхода к квантовой физике Эрвин Шрёдингер, в отличие от Гейзенберга, Паули и Дирака, не был в то время «вундеркиндом». Он скорее принадлежал к поколению Макса Борна и Джеймса Франка, будучи всего на пять лет их моложе: Эрвин родился 12 августа 1887 года.
Как и Вернер Гейзенберг, Эрвин окончил классическую гимназию, где основными предметами были латынь и древнегреческий, и получил основательное гуманитарное образование. Кроме древних языков, он владел в совершенстве английским, испанским и итальянским. По словам его жены, он всегда был первым учеником в классе [5].

Так же старательно он учился в Венском университете, занимаясь теоретической физикой под руководством профессора Фрица Хазенёрля и экспериментальной физикой под руководством профессора Франца Экснера. В год поступления Шрёдингера в университет покончил с собой директор физического института и профессор кафедр теоретической физики и натурфилософии Людвиг Больцман. Тем не менее его влияние в Венском университете продолжало ощущаться. Во вступительной речи в Прусской академии наук Эрвин Шрёдингер вспоминал:
«Старый венский институт Людвига Больцмана, незадолго до моего появления так трагически ушедшего из жизни, где трудились Фриц Хазенёрль и Франц Экснер и через который прошли многие другие ученики Больцмана, дал мне возможность проникнуться идеями этого могучего ума. Круг этих идей стал для меня как бы первой любовью в науке, ничто другое меня так не захватывало и, пожалуй, никогда уже не захватит» [6, с. 339].
На долю поколения Эрвина выпала Первая мировая война. Приват-доценты Борн, Франк, Шрёдингер служили на фронте. С окончанием войны в 1918 году распалась Австро-Венгерская империя, и вернувшемуся в науку Шрёдингеру профессорской должности на родине не нашлось. Обещанное ему место в Черновицком университете оказалось в другом государстве. В Германии, проигравшей войну, тоже свирепствовала инфляция, но положение было всё же лучше, чем в Австрии.
В 1920 году Шрёдингер женился на Аннемари Бертель. Затем поработал короткое время в университете Йены ассистентом Макса Вина, двоюродного брата профессора Вильгельма Вина из Мюнхена, позже получил должность экстраординарного профессора в Штутгарте и, наконец, ординарного профессора в Бреслау. Летом 1921 года поступило очень заманчивое предложение из Цюриха занять кафедру теоретической физики, первым экстраординарным профессором которой в 1909 году стал Эйнштейн. Эрвин оказался третьим профессором теоретической физики в этом университете (вторым был Макс фон Лауэ).
Назначение в Цюрих было для семьи Шрёдингеров подарком судьбы. Вокруг возвышались любимые им горы, воздух был целебен для его больных легких, а оклад швейцарского профессора не шел ни в какое сравнение с заработками немецких или австрийских коллег. Тем не менее богачом он себя не считал. Дух времени хорошо ощущается в письме Арнольду Зоммерфельду, написанном 7 марта 1925 года:
«Сердечный привет от моей жены. Она сегодня на балу… Звучит это немного анахронично, но это ее первый бал, так как время ее юности пало на военные годы, а после войны было не до балов. Честно сказать, я и сейчас считаю их чушью и предпочитаю студенческую вечеринку в немецком или австрийском стиле „утонченному“ цюрихскому балу, где местные денежные аристократы красуются в ложах за 300 франков, а человек вроде простого профессора для них бедняк и плебс. Поэтому я позволил ей идти одной под крылышком Майера, Бера и Шерера — кроме того, входной билет за 25 франков, помноженных на два, — это слишком дорого для такого сомнительного удовольствия» [7, с. 81].
Эрвин тоже вполне мог уехать на курорт один — точнее, с очередной подружкой. В личных делах супруги предоставляли друг другу полную свободу.
В целом Цюрих оказался подходящим местом для этой австрийской пары. Немаловажным для Эрвина было и научное окружение. Особенно близкие отношения сложились у физика Шрёдингера с математиком Германом Вейлем. Впоследствии Аннемари вспоминала в интервью с Томасом Куном:
«Мы все вместе были хорошими друзьями1, и, конечно, Вейль очень интересовался работами моего мужа. Эрвин был очень, очень рад, что Вейль ему так много помогал и что он мог с ним говорить в любое время» [5].
Особенно пригодилась помощь Вейля в период работы над волновой механикой. Друзья-коллеги договорились, что будут обсуждать возникающие проблемы в определенный день недели. Каждый вторник, по вечерам, они встречались, и Эрвин рассказывал о достигнутых результатах, а Вейль помогал выбраться из возникших математических трудностей.
На рождественские каникулы в конце 1925 года Шрёдингер уехал отдыхать и кататься на лыжах на знаменитый швейцарский курорт Ароза, столь любимый Томасом Манном, Германом Гессе и другими немецкими писателями и художниками.
Напряженной научной работе на лыжном курорте не помешало, а может, и способствовало то обстоятельство, что на отдых Эрвин поехал не с женой, а с новой молоденькой подружкой. Каникулы прошли результативно: в Арозе Эрвин завершил первую статью по волновой механике [8], а подружка через девять месяцев родила ему ребенка.
Конечно, схема Феликса Блоха, по которой открытие волновой механики совершилось за несколько недель после коллоквиума Дебая, слишком упрощена. Предложение Дебая сделать обзор работ де Бройля не было случайным — он знал, что Шрёдингер интересуется идеями де Бройля и хочет изучить их более тщательно. Сам интерес к работе французского физика-аристократа возник у Эрвина после чтения статьи Эйнштейна «Квантовая теория одноатомного идеального газа», опубликованной в докладах Прусской академии наук 9 февраля 1925 года. В этой статье великий физик упомянул работу де Бройля, о которой ему рассказал Поль Ланжевен, и отметил:
«Я подробнее остановлюсь на этой интерпретации, так как думаю, что здесь мы соприкасаемся с чем-то большим, чем простая аналогия» [9, с. 502].
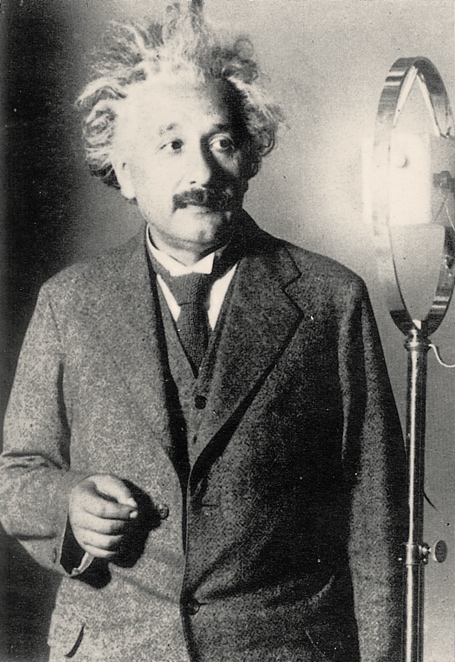
Вот эта фраза Эйнштейна и подтолкнула Шрёдингера вплотную заняться диссертацией де Бройля. Совет Дебая был лишь ожидаемым толчком. О роли Эйнштейна в создании волновой механики Шрёдингер признавался в письме автору теории относительности от 23 апреля 1926 года, когда серия основополагающих статей была почти готова:
«Впрочем, всё это дело не возникло бы ни теперь, ни когда-либо позже (я имею в виду свое участие), если бы Вы в Вашей второй статье о квантовой теории газов не щелкнули меня по носу, указав на важность идей де Бройля» [10, с. 253].
Весь цикл статей Шрёдингера о волновой механике был опубликован в журнале Annalen der Physik в первом полугодии 1926 года. Первая работа была передана в редакции 27 января, шестая — 21 июня.

В первой работе было введено в оборот знаменитое уравнение Шрёдингера относительно некоторой «волновой функции», которую автор обозначил греческой буквой пси. Это обозначение закрепилось за ней и по сей день. Волновая функция, по представлению Шрёдингера, описывала электрон в атоме в виде стоячей волны. Такие волны можно наблюдать у колеблющейся струны скрипки или гитары, издающей звуки разных тонов (частот); среди них выделяются главный тон и обертоны. Такие же частоты у электронов в атоме соответствуют частоте испускаемого или поглощаемого света.
Уравнение Шрёдингера зависит от параметра Е, который означает энергию атома. Оказалось, что уравнение имеет приемлемое решение только при определенных значениях параметра Е, т. е. атом может существовать лишь в заданном наборе стационарных состояний. То, что Нильс Бор постулировал в 1913 году, оказывалось простым следствием уравнения Шрёдингера. В этом была суть волновой механики: не нужно ничего выдумывать и постулировать — знаменитые квантовые условия Бора —Зоммерфельда автоматически вытекали из новой теории австрийского физика из Цюриха.

В кульминационные дни работы над первой статьей Шрёдингер писал 27 декабря 1925 года из Арозы главному редактору журнала Annalen der Physik Вильгельму Вину — тому самому Вину, который чуть не завалил защиту докторской диссертации Вернера Гейзенберга:
«Сейчас меня замучила новая атомная теория. Если бы я только чуть больше понимал в математике! Я в этом вопросе настроен оптимистично и надеюь, что если я только осилю вычисления, то всё будет очень хорошо. Я думаю, что смогу задать колебательную систему — и при этом сравнительно естественным способом, не используя соображений из головы» [7, с. 83].
С математической точки зрения метод Шрёдингера состоял в том, что энергетические уровни — это собственные значения некоторого оператора. Сделав это открытие, он попытался применить его к атому водорода, учитывая релятивистскую механику движения электрона. Но здесь его ждало жестокое разочарование — результаты расчетов не совпадали с опытными данными. Расстроенный Шрёдингер забросил работу, посчитав свой метод ошибочным. На самом деле причина была в другом: метод был хорош, но не был учтен спин электрона — это понятие к тому времени еще не вошло в научный оборот.
Только через несколько месяцев, во время рождественского отдыха в Арозе, Эрвин вернулся к атому водорода, но без релятивистских эффектов, и метод сработал: результаты оказались точно такими, как у Нильса Бора в его первой работе о спектрах атомов, т. е. точно совпадающими с экспериментальными значениями (знаменитая формула Бальмера). Так с задержкой в несколько месяцев мир узнал о волновом уравнении Шрёдингера.

Через месяц после первой статьи «Квантование как задача о собственных значениях» в том же журнале Annalen der Physik появилось «второе сообщение» на ту же тему. В примечании к статье автор подчеркивал, что для ее понимания чтения первого сообщения не требуется. Более того, чисто логически вторая часть должна была бы предшествовать первой, так как здесь Шрёдингер описывает общую методику построения волновых уравнений, опираясь на найденную еще сто лет назад ирландским математиком и физиком Уильямом Гамильтоном аналогию между оптическими и механическими явлениями. Как геометрическая оптика, изучающая законы преломления и отражения лучей, является предельным случаем волновой, занятой интерференцией, дифракцией и рассеянием света, так и волновая механика, по представлению Шрёдингера, является обобщением классической механики. А разработанный Гамильтоном математический аппарат, применяемый и в геометрической оптике, и в классической механике, должен давать аналогичные результаты, если его применить как в волновой оптике, так и в волновой, т. е. квантовой, механике. Это позволило Шрёдингеру применить свой метод для более сложных систем, чем атом водорода, — практически для любых атомных объектов. Результаты оказались очень обнадеживающими. В письме профессору Вильгельму Вину от 22 февраля 1926 года, за день до поступления второй части статьи в редакцию Annalen der Physik, Эрвин делится своей радостью:
«Для меня время летит как на крыльях. Каждый второй или третий день снова приносит какую-то новость — „это“ работает, не я. „Это“ — великолепная классическая математика и гильбертовы пространства, чудесное здание теории собственных значений. Она разворачивает перед вами всё так ясно, что остается только принять результаты без усилий и забот… Я так рад, что этой ужасной механики, кажется, удалось избежать, с ее переменными действиями и вращательными моментами, а также с теорией возмущений, которую я никогда по-настоящему не понимал. Сейчас всё стало линейным, всё следует одно из другого, рассчитывается всё так же легко и приятно, как в старой акустике» [7, стр. 86].

Ссылка на акустику здесь понятна: еще во время Первой мировой войны Эрвин приобрел опыт решения задач по распространению звука и опубликовал несколько научных работ на эту тему.
Евгений Беркович
1. Виталий Лазаревич Гинзбург. К 100-летию со дня рождения. Книга-альбом / Авторы-сост. В. М. Березанская, М. А. Лукичёв, Н. М. Шаульская. М.: издательство «РМП», 2017.
2. Де Бройль Л. По тропам науки. М.: Изд-во иностранной литературы, 1962.
3. Де Бройль Л. Избранные научные труды. Т. 4. М.: Принт-Ателье, 2014.
4. Bloch F. Reminiszenzen an Werner Heisenberg und die Frühzeit der Quantenmechanik // Ch. Kleint, H. Rechenberg und G. Wiemers (Hrsg.). Werner Heisenberg 1901–1976. Leipzig: Verlag der Sächsischen Akademie der Wissenschaften zu Leipzig, 2005. S. 240–246.
5. Annemarie Schrodinger. Interviewed by Thomas S. Kuhn. 5 April 1963 // American Institute of Physics. Oral History Interviews.
6. Вступительная речь Э. Шредингера в Прусской академии наук // Избранные труды по квантовой механике. М.: Наука, 1976. C. 339–342.
7. Hermann A. Die Jahrhundertwissenschaft. Werner Heisenberg und die Physik seiner Zeit. Stuttgart: Deutsche Verlags-Anstalt, 1977.
8. Schrödinger E. Quantisierung als Eigenwertproblem (Erste Mitteilung) // Annalen der Physik. 1926. Vierte Folge. Band 79. S. 361–376.
9. Эйнштейн А. Квантовая теория одноатомного идеального газа. Второе сообщение // Собрание научных трудов в 4 т. Т. III. М.: Наука, 1966. С. 489–502.
10. Джеммер М. Эволюция понятий квантовой механики / Пер. с англ. В. Н. Покровского. Под ред. Л. И. Пономарева. М.: Наука, Главная редакция физико-математической литературы, 1985.
1 У Аннемари был многолетний роман с Вейлем, но отношения между учеными от этого не охладели.

 (5 оценок, среднее: 4,60 из 5)
(5 оценок, среднее: 4,60 из 5)
В интерпретации Шрёдингера квадрат волновой функции пропорционален плотности энергии и массы физического поля, а частица обладает полевой и волновой природой. В интерпретации де Бройля, упрощенно говоря, волна-пилот окружает частицу – меньших размеров или точечную.В копенгагенской интерпретации волновая функция – формальный математический прием, рассчитывающий вероятность обнаружения точечной частицы, а коллапс волновой функции связан с уточнением положением частицы при измерении. У Шрёдингера и де Бройля волновая функция описывает реальный колебательный процесс, а ее коллапс – реальные скачкообразные изменения этого процесса. Шрёдингер считал матричную механику формальным математическим приемом.
Уравнение Шрёдингера – нерелятивистская форма уравнения Клейна-Гордона-Фока, в которое входит третье дополнительное слагаемое с массой покоя по сравнению с уравнениями Максвелла. Все эти уравнения – гиперболические уравнения или уравнения второго порядка, которые описывают большинство колебательных процессов в природе.
Подход Шрёдингера, который долго считался далеким от мейнстрима по сравнению с преобладающей копенгагенской интерпретацией, сейчас снова набирает популярность в мире. Эти интерпретации обычно называют “объективной редукцией”, считая, что волновая функция и ее коллапс (редукция) описывают реальные колебания и их скачкообразные изменения. К таким интерпретациям относятся транзакционная интерпретация, интерпретация Джабса, согласно которой скачкообразное изменение волновой функции происходит при взаимодействии частиц и наложении волновых пакетов, “римская” интерпретация, предполагающая гравитационную природу коллапса волновой функции, и похожая точка зрения Пенроуза.
Простите, а имеются ли, поставлены или же подготовляются / планируются опыты для опытного выявления преимуществ (хотя бы, не говоря о так называемой математической возможной категоричности) той или иной из указанных Вами интерпретаций?
“Господь Бог (конечно – Л.К. – это именно Его прерогатива, полагаю! Впрочем, Его пути…) изощрён, но не…”
Можно ли выявить наиболее на настоящий момент адекватную интерпретацию? Может, Эйнштейновские скрытые параметры и не столь плохи? Достаточен ли в принципе уровень современных физических воззрений для экспериментальных проверок подобного рода?
Л.К.
Пишущий, как Вы поняли, математик по профессии.
Очень ценю вклад покойного проф. Шрёдингера, в одной из “нобелиатских” работ доказавшего, насколько мне известно, взаимную выводимость своего метода с матричным методом Гайзенберга (- Борна – Паскуаля Йордана) и, соответственно, операторным методом Дирака.. Последователем выступил сравнительно недавно ушедший Фримен Джон Дайсон (по математике ученик Абрама Самойловича Безиковича по Кембриджу) с установлением “мостов” и “консолей”, как он сам писал, в трёх различных первоначально трактовках квантовой электродинамики.
Похоже, госп. Шрёдингеру сильно помогло не только непосредственное по Цюриху общение с Германом Вейлем, но также вышедший вовремя “толстотомник” условно “Курант – Гильберт” по методам математической физики, только я не помню, до или после серии нобелиатских Шрёдингеровских статей.
То, что он исходил из де Бройлевской идеи при написания (квази-) волнового уравнения, это, видимо, общее место. Как и последующий прочсёт энергетического спектра водородоподобного атома с установлением “на конце пера” закона Бальмера.
К.
“Как и последующий просчёт энергетического спектра водородоподобного атома с установлением «на конце пера» закона Бальмера.”
Леонид Маркович!
Как Вас понимать? — формула Бальмера была “угадана” в 1885 г. Всё потом из неё и разворачивалось.
…Уравнение Шрёдингера — нерелятивистская форма уравнения Клейна-Гордона-Фока, в которое входит третье дополнительное слагаемое с массой покоя по сравнению с уравнениями Максвелла. Все эти уравнения — гиперболические уравнения или уравнения второго порядка, которые описывают большинство колебательных процессов в природе.
А ничего, что там производная по времени – первого порядка, как в параболических уравнениях? И что никаких колебаний оно не описывает, а только некоторую периодичность в пространстве в определенных случаях? Может, вам лучше про политику тут писать?
Возьмём интерферометр Майкельсона с разницей плеч 1 метр, лазер в качестве источника излучения и ячеку Керра в качестве затвора с временем 10 в минус девятой секунды. Ячейка Керра будет резать луч на кусочки длиной 30 см. Не думаю, что это кто-нибудь когда-то делал, но сомнений, что интерференционная картинка возникнет, вряд ли у кого-то будет.
Так если она, эта картинка, будет — какой интерпретацией её можно объяснить? Что с чем интерферировать будет, если кусочек луча 30 см, а разница плеч 1 м, а скорость света не бесконечна?
Сомневаюсь, что будет интерференция. Если будет, то скорее всего в момент поглощения за счет коллапса волновой функции, который с точки зрения транзакционной интерпретации происходит быстрее скорости света в вакууме. Он не нарушает СТО, так как является вероятностным процессом без причинно-следственной связи. Транзакционная интерпретация предполагает обратный ход времени при сверхсветовом коллапсе.
А Вы не слыхали об интерференции на исчезающе малом космическом излучении (D-линия натрия)? Это всё исследовали, когда думали, что интерференция — многокомпонентный эффект. Ну и запускали в интерферометр по одному кванту. Естественно, каждый из них давал на экране (на фотопластинке) одну единственную точку. Но когда точки поднакопились, оказалось, что образуется старая добрая интерференционная картинка. В эксперименте, который я описал, никакого принципиального отличия от интерференции на исчезающе малой интенсивности нет.
Так что интерференция-то будет. Но ни в какие “интерпретации” она не влезает.
Было бы интересно пронаблюдать поведение дымовых колец на двух щелях. То есть макрокартинку с возможностью съемки на простой телефон (если угодно). С моделированием принципа неопределенности путем покачивания дымовой пушки. Думаю, здесь тоже будет “интерференция” — как с D-линией натрия. Но физики народ занятой и заниматься этим не будут.
В начале восьмидесятых в серьезных журналах (УФН, например) обсуждали проблему интерференции, связывая её с геометрией интерферометров (то есть, откровенно говоря, со структурой пространства). Но тоже дело заглохло.
В христианской догматике принцип неопределенности, который имеет непосредственную связь с интерференцией, — фундаментальное свойство природы, а не следствие нашего воздействия на систему в результате измерения (Шестой Вселенский собор, догмат о двух волях во Христе, который приводит к воле, как имманентному свойству материи. То есть к отсутствию детерминизма на уровне микромира и к принципиальному несохранению информации. И, как следствие, к отсутствию времени, как онтологической реальности). Но кто же из серьезных людей будет думать над догматом о двух волях во Христе? Серьезные физики (разве что за исключением 7-ого герцога Брольи и Леметра. Ну, ещё Эйнштейна, может быть) христиан недоумками считают.
Эксперимент по интерференции как доказательство бытия Божьего – это сильно!
Похоже, богословие вообще впереди науки всей. ))
Физики используют дуализм «волна=частица», но пока не осилили богословский догмат триединства «Отец=Дух*Сын» – например, в формате «Информация=Энергия*Вещество».
Химики в кинетике обходятся бинарными столкновениями частиц, а тройными и более только в полуэмпирических теориях катализа – там без них никак.
Троичный квантовый компьютер в очереди на рождение на стыке наук…
Не исключено, – и Троица не конечный вариант богословского творчества в описании дуализма «Бытие=Небытие», который, в свою очередь, похоже, допускает тринитарное обобщение…
Уважаемые господа Лебедев и Аксайский!
Ирония- чудесная вещь. Но физик, прежде чем иронизировать, должен, как мне кажется, избавиться от сингулярностей. Я понимаю — в своём обществе ко всему привыкнуть можно, даже к сингулярности. Но если со стороны — неприлично.
По мне, так ирония, особенно самоирония, и есть способ избавления от сингулярностей, – когда ум за разум заходит. Мне помогает ))
Насчет интерпрпетации КМ полезно почитать последние работы В.И. Манько сотоварищи. Он таки придумал, как ввести в КМ классическую вероятность, чтобы )) его студентам было проще погружаться в пучину КМ. Там у него математика не совсем простая, но вполне осиливаемая.
Чуть поконкретнее, please!
Заранее спасибо.
Л.К.
Google – манько квантовая механика интерпретация
Не поверите, как много можно узнать в гугле )) Я даже так ссылки для реальной работы нахожу.
Спасибо!
Л.К.
Учтём. Как там с аффтарским правом буде(т)?
Перевирая В.Высоцкого, дескать, “ты желаешь мне Гугля, ах ты…!”
К.
У нас преподавал физическую химию человек по фамилии Гугля. Он меня на нее и “подсадил”.
И вы, студиозусы, звали его промеж себя, верно – “гугля – мугля”?
(ритор вопр)
Л.К.
Нет. Он был величественен и строг, росту небольшого и был женат на студентке нашего факультета с предыдущего курса. Пятерок не ставил почти никогда. Я просел на вопросе: откуда берет энергию концентрационный электрический элемент?
Вы, часом, с концлагерем, не спутали типа?
Л.К.
Там всё просто минус баланда. Имхо.
К.
Программа “Антиплагиат” разберётся ))
Да, этот чел:
http://wikimipt.org/wiki/Манько_Владимир_Иванович
начинает мне типа “ндравиться”. Потихоньку. Дойду ли я до должной
типа кондиции, чтоб читать его работы?:
https://ru.m.wikipedia.org/wiki/Манько,_Владимир_Иванович
Не факт, ой, не факт!
Всё равно, спасибо!
Л.К.
Восхищает первый комментарий Максима Т., – он мгновенно ассоциировался с Нильсом Бором. По слухам, Нильсу Бору не было равных в умении запутывать мозги всем, кому повезло внимать его рассуждениям вслух.
Из вики-статьи: Квантовая запутанность — квантовомеханическое явление, при котором квантовые состояния двух или большего числа объектов оказываются взаимозависимыми. Такая взаимозависимость сохраняется, даже если эти объекты разнесены в пространстве за пределы любых известных взаимодействий. ))
Только в случае полного выключения внешнего взаимодействия ;)
…Восхищает первый комментарий Максима Т., — он мгновенно ассоциировался с Нильсом Бором.
Бор тоже не отличал параболических уравнений от гиперболических?
На то был Хендрик Крамерс (который с Ванье и без, “и так неплох на вид” по В.В. Маяковскому из “Юбилейного”, кажется).
Л.К.
Заглянул в его печатные труды на русском. Вывод: различал и применял, но весьма экономно – похоже, не увлекался математической техникой.
На то был брат, Харальд, известная личность и приятель самого Харди.
Проф. Исидор Натансон назвал именем Гаральд своего сына (мама Г.Я. Перельмана аспиранствовала – у сына, который Гаральд, проживший 1930 – 2003).
Так что младший брат Нильса Бора разбирался и вполне в этих “материях”, самому Нильсу это было не слишком, полагаю, нужно. Обходился и вполне себе.
Так считаю.
Л.К.