Эта заметка посвящена тому, как люди, разделенные континентами, решали и решили разными способами и довольно быстро одну задачу. Предварительно опишу, к какому типу она относится. Процитирую фрагмент книги «Шахматы. Математика. Компьютеры» 1 Евгения Яковлевича Гика.
 «Множество интересных задач и головоломок в шахматной математике возникает при решении следующих двух комбинаторных проблем.
«Множество интересных задач и головоломок в шахматной математике возникает при решении следующих двух комбинаторных проблем.
1. Какое наибольшее число одноименных фигур (коней, ферзей, ладей, королей и слонов) можно расставить на доске так, чтобы никакие две не угрожали друг другу?
2. Какое наименьшее число одноименных фигур (коней, ферзей, ладей, королей и слонов) можно расставить на доске так, чтобы они держали под контролем все свободные поля?»
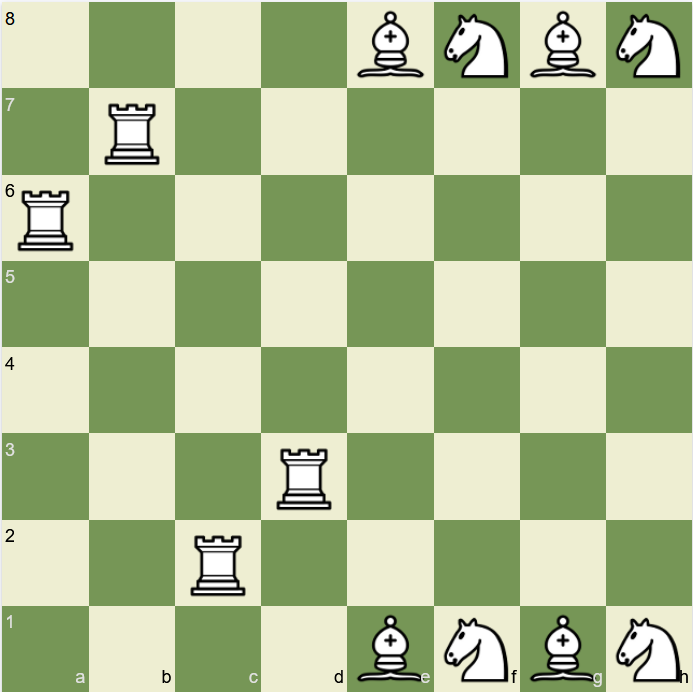
Вот пример одной из таких задач в этой книге: «При каком наибольшем P на обычной доске можно расставить P ладей, P слонов и P коней так, чтобы ни одна из фигур не угрожала другой?» Ответ там же: при P = 4 (всего 12 фигур).
Мне же пришла идея задачи другого рода. Ни в книге Е. Я. Гика, ни в других источниках я не встречал задач на такой тип доминирования фигур.
Задача о замощении доски цепочками фигур, бьющих друг друга по кругу
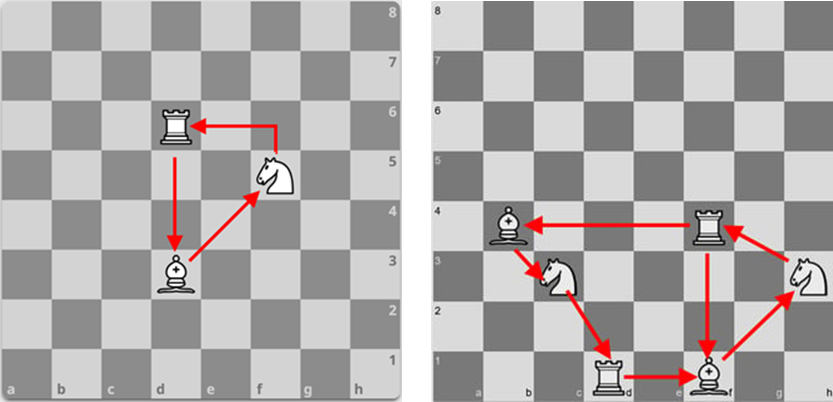
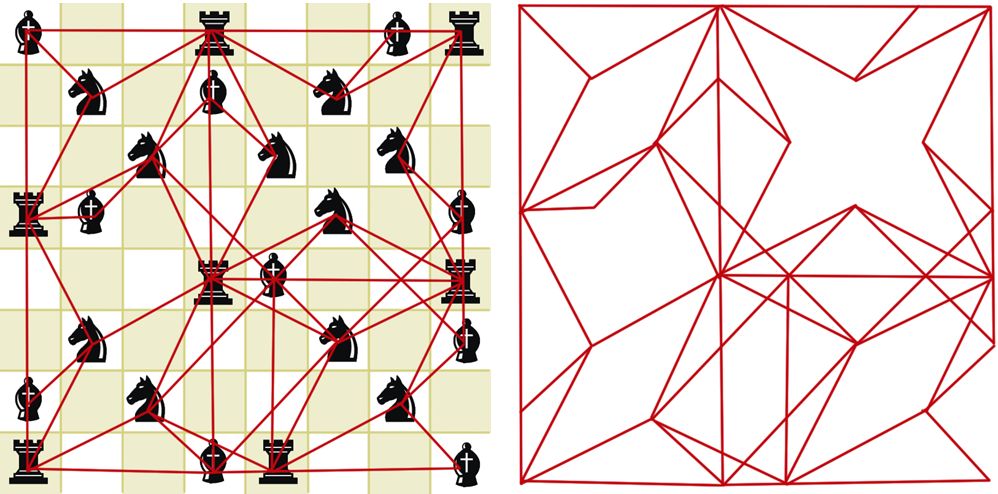
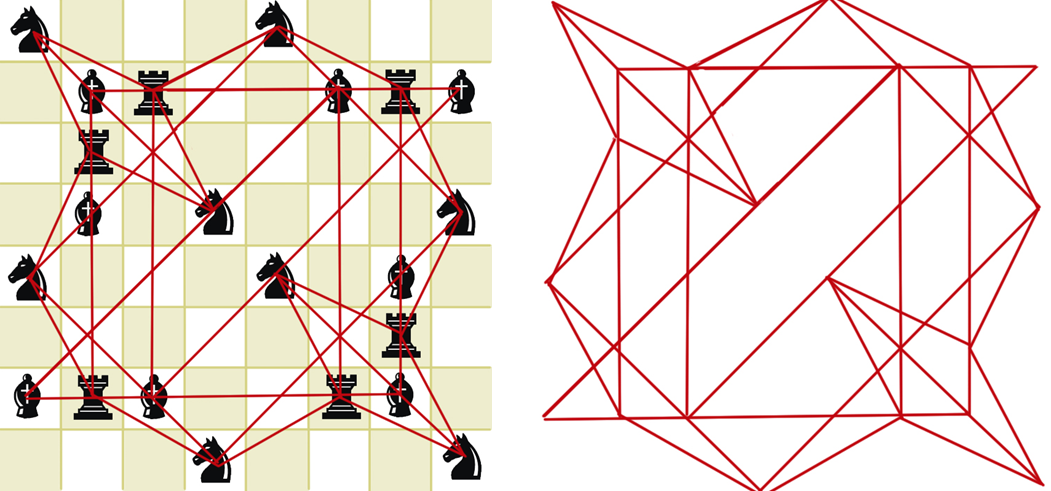
Например, слона, коня и ладью можно поставить на доску так, что они будут атаковать друг друга по принципу «камень, ножницы, бумага»: слон бьет коня, конь — ладью, ладья — слона (круг замкнулся). На диаграммах ниже показаны два цикла такого типа — самый короткий (слева) и подлиннее (справа).
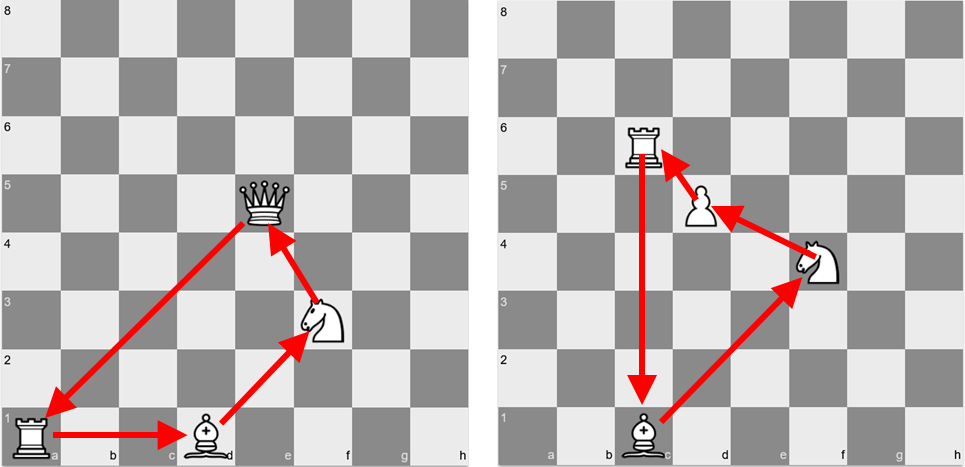
Можно по такому же круговому принципу расставить и четыре фигуры, добавив ферзя: ферзь → ладья → слон → конь → ферзь. Или использовать вместо ферзя пешку.
Но вернемся к трем фигурам — с ними проще. Придуманная мной шахматно-математическая задача была такой.
Какое максимальное количеством слонов, коней и ладей, бьющих друг друга по принципу «камень, ножницы, бумага», можно разместить на шахматной доске 8×8?
Путь к ответу и найденные компьютерные решения
Я воспользовался возможностью задать вопрос на английском на портале Mathematics 2. После описания условия, показа диаграмм и той формулировки вопроса, данной выше, я дописал следующее (это важно, как станет ясно ниже).
«Идею можно развить.
2. Каковы решения для всех возможных комбинаций K типов фигур (3 ≤ K ≤ 6), включая, например, пешки, ферзей и королей? (В шахматах есть шесть типов фигур: пешки, слоны, кони, ладьи, ферзи и короли.)
3. Каково обобщение для шахматных досок N×N и M×N? Для цилиндрических шахматных досок N×N и M×N?
О нетранзитивных (по типу «камень — ножницы — бумага») отношениях не отдельных шахматных фигур, а расстановок белых и черных см. “Intransitively winning chess players positions”»3.
Один из редакторов портала через несколько минут отправил задачу мне на редактирование, порекомендовав сделать ее более прицельной. Я убрал то, что написал о развитии идеи, и задаче был дан ход — она появилась на портале.
Тут же появились доброжелательные комментарии с вопросами и уточнениями. Задачу в тот же день решил доктор математики под ником RobPratt (США), специализирующийся в том числе на линейном программировании. Ценные комментарии сделали (перечисляю в алфавитном порядке латиницей) anankElpis (страна не указана), Bruno Andrades (Бразилия), CiaPan (страна не указана), Ethan Bolker (США), Gerry Myerson (Австралия). Я всем им очень признателен.
Вначале RobPratt предложил переформулировать вопрос задачи. Стало так.
Каково максимальное количество фигур (слон, конь, ладья) на шахматной доске 8 × 8 при условии, что каждый слон атакует по крайней мере одного коня и подвергается нападению по крайней мере одной ладьи, каждый конь атакует по крайней мере одну ладью и подвергается нападению по крайней мере одного слона, и каждая ладья атакует по крайней мере одного слона и подвергается нападению по крайней мере одного коня?
Это то же самое, что я имел в виду вначале? Это равносильные формулировки? Показалось, что да. Но потом выяснилось, что переформулировка привела не совсем к тем результатам, которые я имел в виду.
А пока никто не предложил решения, CiaPan, не видевший, как и другие, мой текст о развитии идеи задачи (я же его удалил, делая задачу более прицельной), спросил меня: «Вы рассматривали возможность использования пешек? Благодаря их асимметрии вы можете легко создавать цепочки „пешка → пешка → … → пешка“ разной длины (предварительно определив их направление — вверх или вниз по доске)».
Я: «Спасибо за интересную идею. Это может быть следующей задачей, которую нужно решить. В первом варианте задачи я написал: 2. Каковы решения для всех возможных комбинаций K типов фигур (3 ≤ K ≤ 6), включая, например, пешки, ферзи и королей?» (то есть вернул-таки удаленное, но не полностью и в другое место).
Были и другие комментарии и вопросы.
К концу того же дня RobPratt дал ответ на им же переформулированный вопрос: замостить можно всю доску (64 клетки). Получилось красиво: любой угловой квадрант 4×4 повторяется один раз со сдвигом, один раз в зеркальной симметрии и один раз в центральной симметрии относительно центральной точки доски. И найдено это решение, повторю, линейным программированием.
Но как такие решения могут получаться? Появились вопросы комментаторов к RobPratt о том, как он использовал линейное программирование. Он сослался на решатель The Mixed Integer Linear Programming Solver и привел математическое описание двоичных переменных для этой задачи.
Но! Приглядевшись к решению на доске, можно видеть, что кони здесь бьют (едят) не только ладей, но и других коней, а слоны — других слонов, т. е. ладьи и кони при такой расстановке занимаются каннибализмом. (Это выражение Татьяны Бонч-Осмоловской, подключившейся к задаче позднее в другом формате — по электронной почте.)
Ладьи безупречны в отношении каннибализма (друг друга не едят), но бьют не только слонов, как хотелось бы, но и коней. Аналогично, кони бьют не только ладей (опять-таки, как хотелось бы), но и слонов. Таково было следствие переформулировки вопроса задачи от RobPratt.
Этот факт избыточных атак наряду с нужными был прокомментирован (вот чем хорошо решение в полилоге — разговоре многих участников). anankElpis написал: «Возможно, для большего соответствия первоначальной идее задачи было бы лучше, если бы ладьи не атаковали заодно и коней, и то же касается других фигур. Тогда атаки были бы только в цикле типа ладья → слон → конь → ладья. Хотя это значительно усложняет задачу».
Я ответил, что согласен.
И RobPratt дополнил решение: «С учетом дополнительных требований, что слоны атакуют только коней, кони атакуют только ладей, а ладьи атакуют только слонов, максимальное количество фигур оказывается равным 30».
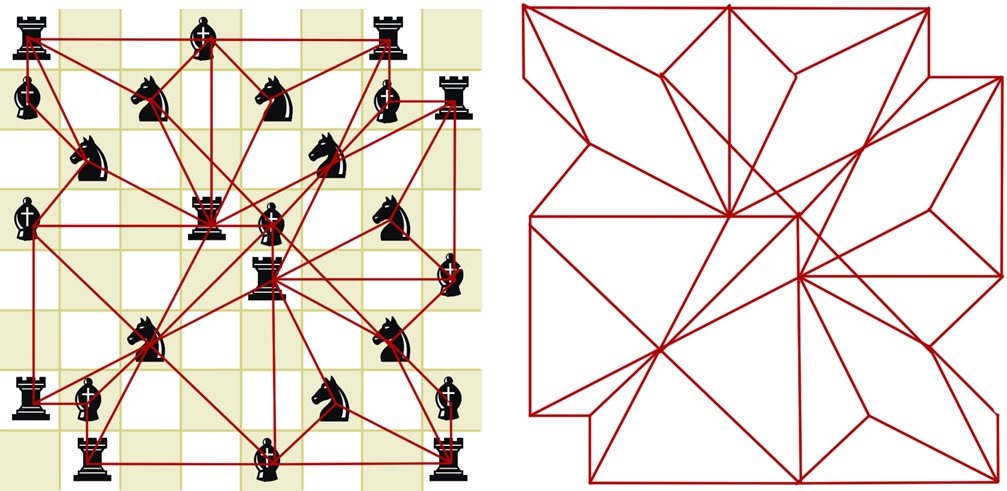
Значит, если эти дополнительные требования и усложнили ему задачу, то не сильно. Вот решение от RobPratt, полученное опять-таки линейным программированием. И снова получилось красиво: каждая фигура имеет пару — такую же фигуру, симметричную относительно центральной точки доски. Может быть, компьютер выдал ему множество решений, а он из них выбрал именно это как симметричное, — не знаю.
Слева — решение от RobPratt, справа — его роспись графами от Татьяны Бонч-Осмоловской.
Я стал делиться задачей и решениями RobPratt от со знакомыми. Откликнулось несколько человек, я напишу в этой заметке об одном ответе.
Красота ручной работы
Как уже понятно, откликнулась Татьяна Бонч-Осмоловская — российская и австралийская писательница, поэтесса, переводчица и художница4 . Что важно здесь — выпускница школы-интерната им. А. Н. Колмогорова МГУ им. М. В. Ломоносова с углубленным изучением математики, физики, химии, биологии, информатики, а затем — выпускница МФТИ. Вот некоторые из ее картин на тему шахмат 5.
Если присмотреться к центру поля, можно увидеть всё уменьшающиеся доски с фигурами. Фрактальная геометрия этих шахматных досок создает свои смыслы. Какие?
На втором рисунке фигуры шахматного куба внутри и вне его одновременно (угол в центре может восприниматься и как самый ближний к зрителю, и как самый дальний). За кого играет красная королева? Ответа нет — это не шахматная задача. Какие смыслы эта картина порождает?
Вот некоторые предложенные Татьяной решения задачи. Для начала она построила расстановку для первой формулировки от RobPratt и тоже заполнила всю доску.
Как пишет Татьяна Бонч-Осмоловская, симметрия здесь только сдвиговая (все угловые квадранты 4×4 повторяют друг друга со сдвигом), в отличие от решения от RobPratt.
Затем она занялась решениями под вторую, более точную формулировку вопроса.
Здесь 25 фигур, и тоже симметрия, но не по всей доске.
Еще одно ее решение:
Здесь 27 фигур (до 30 от RobPratt недалеко). Татьяна Бонч-Осмоловская отмечает, что на схеме видны довольно интересные локальные закономерности, но общей симметрии нет.
А вот ее решение с 22 фигурами — зато полностью симметричное. Она пишет: «Может быть, я изначально шла не за количеством, но за красотой и симметрией — и смотрите, какой совершенно центрально симметричный рисунок с рядом внутренних зеркальных симметрий! У меня фигуры „плотнее“: скажем, каждый конь бьет по две ладьи. А у RobPratt — по одной».
Также она прислала ряд других интересных решений с объяснениями их особенностей, но я не привожу их из-за ограничений по объему.
Здесь можно задаться вопросом — зачем придумывать расстановки самим, когда «нам алгоритмы сделать всё сумеют»? Кому-то интересно решать задачи через изобретаемые алгоритмические структуры, кому-то — всё делать самому от начала до конца. И расставляя и прорисовывая всё самостоятельно (если время позволяет), лучше понимаешь закономерности — есть такая гипотеза.
Были и другие отклики, о них я напишу в другой раз.
Заключение
В целом, я думаю, что у этой задачи и у других задач на атаки разных фигур в цикле «камень, ножницы, бумага» есть перспективы. Напомню хотя бы о возможном расширении на другие фигуры (от пешек до королей) и другие размеры и формы шахматных досок. Можно проводить сравнения результатов заполнения доски цепочками, в которых добавляется, а потом меняется только один элемент:
1. ладья → слон → конь → ладья
2. ладья → слон → конь → ферзь → ладья
3. ладья → слон → конь → пешка → ладья
В общем, можно по-всякому отважно резвиться…
Александр Поддьяков, докт. психол. наук
1 Гик Е.Я. Шахматы. Математика. Компьютеры / ред. А. Ханян. — Изд. Андрей Ельков, 2013.
Е.Я. Гик (1943–2016) – советский и российский шахматист и шахматный литератор, мастер спорта СССР (1968). Математик; кандидат технических наук. Участник чемпионата СССР (1967). Обладатель Кубка Москвы (1971). Автор ряда популярных книг по шахматам и другим настольным играм, а также связанным с ними математическим проблемам и головоломкам.
3 Poddiakov A. (2024). Intransitively winning chess players’ positions // Doklady Mathematics, 110 (Suppl 2), S391–S398. doi.org/10.1134/S1064562424702417. Full text: rdcu.be/efzwS.
Версия на русском: Поддьяков А.Н. Нетранзитивные по выигрышности позиции белых и черных в шахматах // Математическая теория игр и ее приложения. 2022. № 3. С. 75-100.
Научно-популярно: Поддьяков А.Н. Позиции белых и черных по принципу «камень, ножницы, бумага» // ТрВ-Наука № 366 от 15.11.2022, с. 11.
4 Поддьяков А. Н. Фрактальная геометрия шахматной доски и сады Семирамиды на ленте Мёбиуса. Игры форм и смыслов в мирах Татьяны Бонч-Осмоловской // Нож. 25 декабря 2021 года.
5 gallery.bridgesmathart.org/exhibitions/2016-joint-mathematics-meetings/tatianabonch