Позиции белых и черных по принципу «камень, ножницы, бумага»

Математические объекты, выигрывающие друг у друга нетранзитивным образом (по принципу «камень, ножницы, бумага» ¹), стали широко известны благодаря колонкам Мартина Гарднера в научно-популярном журнале Scientific American в 1970 и 1974 годах². Он описал, например, необычные, специально изобретенные игральные кубики с разными нестандартными числами на гранях. Благодаря подбору нестандартных чисел игральная кость A чаще выигрывает (показывает большее число на верхней грани при бросках), чем кость B в паре A–B, B чаще выигрывает у C в паре B–C, но C чаще выигрывает у A в паре A–C. Соответственно, при возможности выбора кости, чтобы выиграть, надо выбирать A в паре A–B, B — в паре B–C и C — в паре A–C. А возможна ли нетранзитивность выигрышности позиций сторон в детерминированных стратегических позиционных играх с полной информацией и нулевой суммой — шахматах и шашках?

Здесь необходимо уточнение терминологии. Термин «позиция» в шахматах (и шашках) имеет два разных значения. Первое значение — позиция как целое, объединяющее позиции сторон («На доске возникла интересная позиция»). Второе значению — позиция одной из сторон (одного из игроков). Пример использования термина «позиция» в этом значении: «После неожиданного хода соперника его позиция заметно ухудшилась».

Различая эти два значения, я буду говорить о позициях сторон, или, применительно к шахматам и шашкам, позициях белых и черных. Проведу противопоставление. Вот что пишут о транзитивности позиций как целого.

«Современные схемы компьютерной оценки шахматной позиции основаны на двух допущениях. Во-первых, существует возможность решить, какая позиция благоприятнее, и, во-вторых, это отношение [большей благоприятности] транзитивно. Вследствие этих предположений, число, служащее мерой ценности [позиции], может быть присвоено любой шахматной позиции» ³.

«Конструирование базы шашечных эндшпилей — это просто расчет транзитивного замыкания. Каждая позиция — член множеств побед, проигрышей и ничьих. Информация об однажды рассчитанной и классифицированной по этому принципу позиции, записанная в базу данных, представляет собой совершенное знание теоретической ценности данной позиции» ⁴.

«Имея сеть совершенных оценок, вы можете определить лучший ход в каждой позиции, выбирая действие, ведущее к состоянию с большей оценкой» ⁵.

Для позиций как целостностей транзитивность соблюдается всегда. Я собираюсь ставить под сомнение не это, а транзитивность составляющих позицию как целого — позиции сторон (белых и черных). Я буду делать это с помощью примеров, которые относятся к так называемым неортодоксальным конструкционным. Можно сказать, что примеры нетранзитивных по выигрышности позиций сторон деконструируют шаблон определенной направленности мышления, связанной с ошибочным расширением «школьно понятого» свойства транзитивности превосходства «если A≻B и B≻C, то A≻C» (знак «≻», похожий на «>», означает «превосходить», «быть предпочтительнее» и т. п.).

В математических терминах данные примеры можно отнести к так называемым патологическим. «Термин „патологический“ используется в математике для обозначения примера, специально созданного, чтобы показать нарушение определенных, почти универсальных свойств. Патологические задачи часто позволяют строить интересные примеры контринтуитивного поведения математических объектов. Они также служат прекрасными иллюстрациями того, почему для многих математических утверждений, претендующих на универсальную истинность, требуется очень подробное описание условий применимости» ⁶.

Для практики шахматной игры приводимые неортодоксальные примеры бесполезны. Но они позволяют развить теорию. Я покажу, что классификация позиций должны быть дополнена еще одним основанием — по транзитивности/нетранзитивности выигрышности позиций сторон.

Примеры нетранзитивных по выигрышности позиций сторон

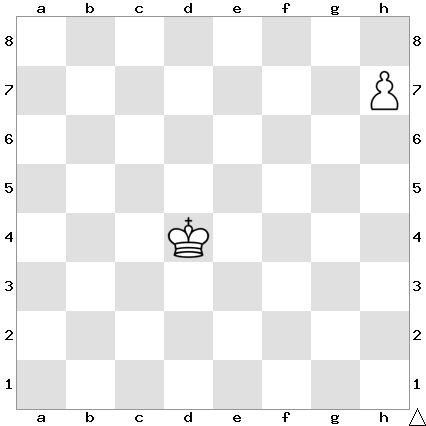
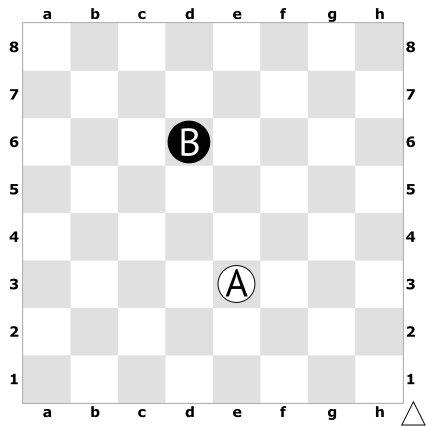
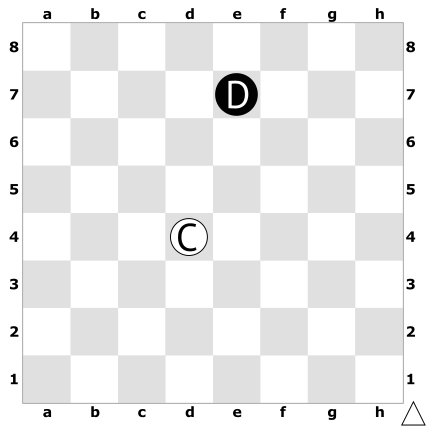
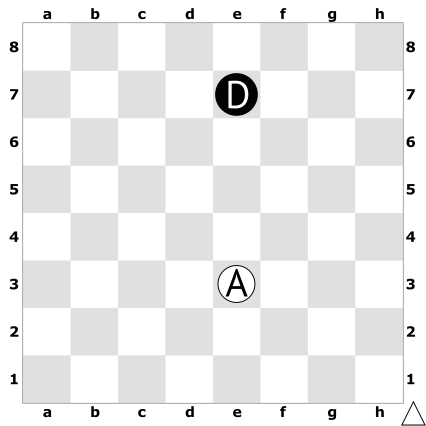
Рассмотрим набор из следующих четырех позиций — две позиции белых (A и C) и две черных (C и D), — который я придумал в 2016 году⁷.

Две шахматные позиции белых и две позиции черных для попарного наложения на одну доску (A и B; B и C; C и D; D и A) и демонстрации образованного ими нетранзитивного цикла по выигрышности (Поддьяков, 2016)

‌

Последовательно наложим эти пары позиций на одну доску.

Позиции A, B, C, D, попарно наложенные на одну доску для демонстрации их нетранзитивности по выигрышности. Белые начинают во всех вариантах в соответствии с правилами шахматной композиции

‌

Решая задачу о том, какая позиция выигрышнее (предпочтительнее) в паре, можно видеть, что:

• позиция A белых предпочтительнее позиции B черных (при возможности выбора игры за белых или за черных надо выбрать позицию A белых);
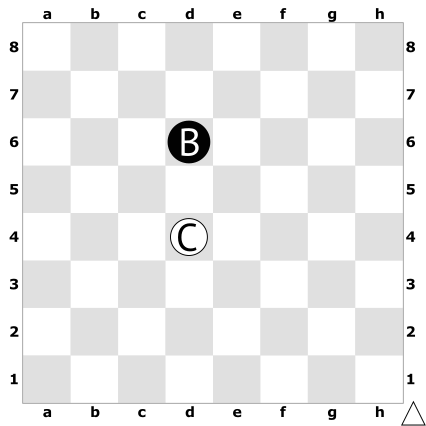
• позиция B черных предпочтительнее позиции C белых;
• позиция C белых предпочтительнее позиции D черных;
• но позиция D черных предпочтительнее позиции A белых.

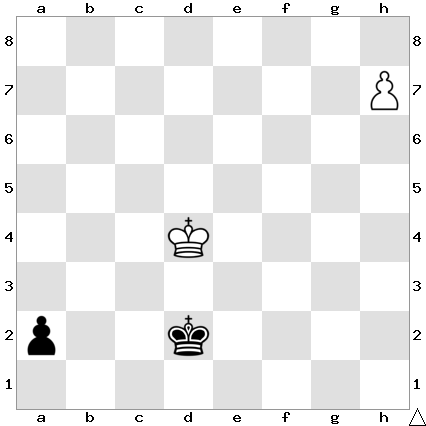
А. Ю. Филатов в развитие идеи нетранзитивных позиций сторон сконструировал минималистскую цепочку из 4 позиций, где с каждой стороны участвуют только король и пешка ⁸. Обращу внимание на то, что позиции белых A и C зеркально симметричны, как и позиции черных B и D, которые тоже зеркально симметричны. При наложении на одну доску симметричны позиции в первом значении (позиция как целое): зеркально симметричны позиции на первой и третьей доске, а также на второй и четвертой.

Минималистская и симметричная структура нетранзитивных по выигрышности шахматных позиций А. Филатова. Вверху — ряд позиций A, B, C, D; внизу — их попарные наложения на одну доску

‌

С использованием нетранзитивности позиций белых и черных могут быть сконструированы различные интересные шахматные задачи. Г. Л. Попов, международный мастер по шахматной композиции, главный редактор шахматного портала SuperProblem, построил следующую задачу и дал ее возможное решение ⁹.

Шахматная задача Г. Л. Попова с использованием нетранзитивных по выигрышности позиций

‌

Сконструированы и шашечные позиции, нетранзитивные по выигрышности сторон, их построил С. Жураховский. Он указал, что те же позиции нетранзитивны и в поддавках. Обратим внимание, что в шашках нетранзитивные позиции могут включать только по одной шашке с каждой стороны.

Нетранзитивные по выигрышности шашечные позиции С. Жураховского, построенные в развитие идеи нетранзитивных позиций в шахматах

‌

Заключение

Классификация позиций должны быть дополнена еще одним основанием — по транзитивности/нетранзитивности выигрышности позиций сторон. Ранее задача конструирования нетранзитивных по выигрышности позиций сторон никем не ставилась. Причина, возможно, в том, что есть справедливое суждение о транзитивности позиций как целостностей. Я ответил дополнением: но есть нюанс — позиции сторон как раз могут быть нетранзитивны, в отличие от позиций как целостностей ¹⁰. Я показал это с помощью придуманного мной неортодоксального конструкционного (в шахматных терминах) и патологического (в математических терминах) примера. Идея оказалась идеепорождающей: она была поддержана и развита двумя шахматистами, придумавшими свои более сложные примеры с обобщениями — А. Ю. Филатовым и Г. Л. Поповым, а также шашистом С. Жураховским, который придумал соответствующий пример для шашек. Абстрактный шахматный и шашечный мир усложнился усилиями нескольких человек.

Была ли исходная идея возможности нетранзитивных по выигрышности позиций игроков так называемым революционизирующим вопросом? Об этих вопросах в шахматах см.¹¹ Поставим планку несколько ниже: полученные результаты могут рассматриваться как еще одно относительно локальное восстание (не революция) против аксиомы транзитивности предпочтений (если А предпочтительнее В, а В предпочтительнее С, то А предпочтительнее С). Она широко используется в теории принятия решений как универсальная, общеприменимая для самых разных областей. На материале позиций сторон в шахматах и шашках ее можно дополнительно проблематизировать (дополнительно — потому что до этого были, например, нетранзитивные игральные кубики).

Возможно, для кого-то из теоретиков шахматной игры эти результаты, увеличивающие разнообразие известных видов отношений между позициями сторон, окажутся заслуживающими внимания. Как минимум оснований для их классификации стало больше.

Александр Поддьяков

Я признателен Михаилу Гельфанду за важные комментарии по статье

¹ Это сокращенная версия статьи: Поддьяков А. Н. Нетранзитивные по выигрышности позиции белых и черных в шахматах // Математическая теория игр и ее приложения. 2022. № 3. С. 75–100.

² Гарднер М. Крестики-нолики. — М.: Мир, 1988; Гарднер М. Путешествие во времени. — М.: Мир, 1990.

³ Atkinson G. Chess and Machine Intuition. — Exeter: IntellectTM, 1998. P. 38

⁴ Lake R., Schaeffer J., Lu P. Solving large retrograde analysis problems using a network of workstations. 1993. P. 3.

⁵ Unzueta D. AlphaGo: How AI mastered the game of Go.

⁶ Weisstein E. W. Pathological // MathWorld — A Wolfram Web Resource.

⁷ Поддьяков А. Н. Нетранзитивность превосходства и ее использование для обмана и тренировки мышления // Психолого-экономические исследования. 2016. Т. 3. № 4. С. 43–50.

⁸ Филатов А. Ю. Нетранзитивные позиции в шахматах // Наука и жизнь. 2017. № 7. С. 117–120.

⁹ Попов Г. Л. Нетранзитивность — кладезь для шахматных композиторов. 2021.

¹⁰ Можно потренировать логику, размышляя над следующим вопросом: почему возможны нетранзитивные позиции сторон при том, что их объединения в целостности на досках занимают свои ранжированные места в транзитивно упорядоченном списке всех возможных позиций (как целостностей)? Может быть, это задача для «Кванта» (после оттачивания формулировки).

¹¹ Васюкова Е. Е. Эвристики мышления // Психология когнитивных процессов. 2020. № 9. С. 129–142; Левидов М. Ю. Стейниц, Ласкер. — М.: Russian Chess house, 2008.