
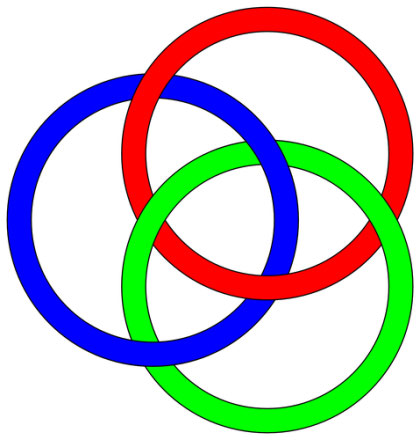
Нетранзитивные отношения доминирования описываются метафорой отношений «камень, ножницы, бумага». Камень, ножницы и бумага в одноименной игре бьют друг друга по кругу и образуют так называемый нетранзитивный цикл доминирования (превосходства). Примеров из различных областей много, приведу яркий (во всех смыслах). Это кольца Борромео — «зацепление, состоящее из трех топологических окружностей, которые сцеплены и образуют брунново зацепление (то есть удаление любого кольца приведет к разъединению двух оставшихся колец). Другими словами, никакие два из трех колец не сцеплены, тем не менее, все вместе они сцеплены» 1.
М. Чемберленд и И. Херман обратили внимание на следующее (вглядимся и убедимся):
- красное кольцо лежит сверху синего («доминирует» над ним, «придавило» его);
- синее кольцо лежит сверху зеленого («доминирует» над ним);
- зеленое кольцо лежит сверху красного («доминирует» над ним).
Круг доминирования замкнулся — получились отношения «камень, ножницы, бумага», что авторы и отразили в названии статьи 2.
Р. Саутвелл, совершенно не рассматривая кольца Борромео в контексте отношений «камень, ножницы, бумага», показал на видео следующую процедуру. Можно сделать кольца Борромео, каждое из которых сплетено из трех других колец Борромео. А каждое из них можно сплести из трех других колец Борромео — и т. д., и т. д., и в результате получается фрактал. Триплет колец Борромео, состоящих из триплетов колец Борромео, рассматривается также в недавней статье 3.

Объединим рассуждения от Чемберленда и Хермана и от Саутвелла. На видео Саутвелла тогда получается, что отношения «камень, ножницы, бумага» вплетены (вложены) в отношения «камень, ножницы, бумага», вплетенные в отношения «камень, ножницы, бумага» — и т. д., и т. д. Это можно считать подводкой к примерам метанетранзитивных отношений доминирования. Только подводкой, потому что кольца Борромео представляются все-таки скорее одной из визуальных метафор нетранзитивных отношений превосходства, ведь реального превосходства там нет («лежать на другом кольце» — это лишь метафорическое превосходство).
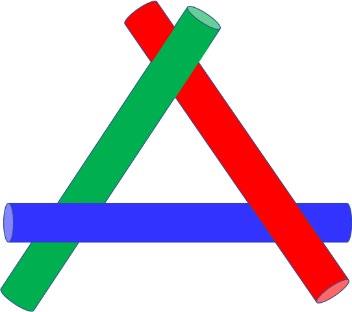
Или не метафорическое? Являются ли три длинных цилиндра (три бревна), положенные так, как показано на рисунке, примером нетранзитивности доминирования (превосходства)? Отношение «лежать сверху» нетранзитивно, но можно ли вести речь о превосходстве? Оставляю решение этого вопроса на усмотрение читателей. Замечу лишь, что если речь идет о материальных тяжелых конструкциях, то да, зеленое бревно может создать критические напряжения в красном бревне под собой и проломить его, красное бревно может создать критические напряжения в синем бревне под собой и проломить его, а синее бревно может создать критические напряжения в зеленом бревне под собой и проломить его.
Вернемся к метанетранзитивным отношениям доминирования. Это нетранзитивные отношения между тремя и более системами, в каждой из которых, в свою очередь, имеются свои вложенные нетранзитивные циклы доминирования между подсистемами — и т.д 4. Было введено понятие уровня (или порядка) метанетранзитивности, определяемого как количество уровней вложенных нетранзитивных циклов. В контексте этого понятия все ранее известные примеры математических нетранзитивных объектов (скажем, все известные наборы нетранзитивных игральных кубиков 5) относятся к метанетранзитивности нулевого уровня (в них нет вложенных нетранзитивных циклов доминирования). В развитие представлений о метанетранзитивности были разработаны примеры метанетранзитивных объектов первого уровня — метанетранзитивных игральных костей (автор — А. В. Лебедев 6) и метанетранзитивных рычагов (автор — А. Н. Поддьяков) со вложенными нетранзитивными циклами.
Из последних результатов — месяц назад я придумал числовые примеры, которые позволяют перейти к метанетранзитивностям второго и более высоких уровней, в пределе — произвольно высокого уровня. Даю ссылки на препринты 7, потому что негуманно приводить здесь девять построенных мною таблиц с девятью трехзначными числами в каждой, иллюстрирующих метанетранзитивность второго уровня. (Есть мнение, что каждая следующая формула в научно-популярной статье уменьшает количество читателей вдвое, а в научных публикациях, например по биологии, каждая дополнительная формула уменьшает цитируемость статьи на 28% 8. Я не собираюсь вносить вклад в эту тему, проверяя, какова доля читателей, уходящих к другим занятиям с каждой последующей таблицей трехзначных чисел.)
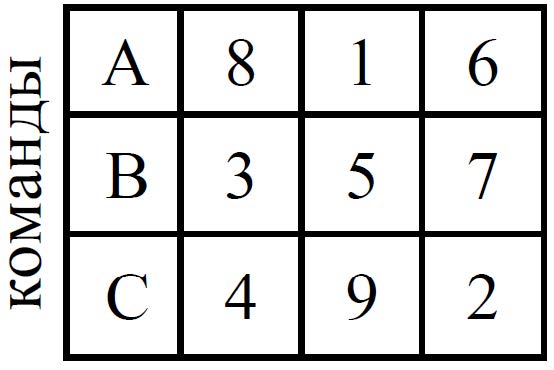
Поясню суть на примере лишь с одной исходной таблицей, известной любителям магических квадратов (таких, в которых суммы по строкам, столбцам и диагоналям равны между собой). Более 60 лет назад Лео Мозер обратил внимание на следующее. Числа в древнекитайском магическом квадрате Ло Шу таковы, что если принять их за силу шахматистов трех команд, то в круговом турнире, где каждый шахматист одной команды встречается с каждым шахматистом из других команд, первая команда выиграет у второй со счетом, кратным 5:4, вторая — у третьей с таким же счетом, а третья — у первой с тем же счетом 9.
Разовьем этот пример для метанетранзитивности.
Предположим, в шахматных турнирах разного уровня встречаются школьники-шахматисты из трех школ, от каждой школы — по три класса. Мои результаты показывают, что школьники одной школы могут чаще выигрывать у школьников другой школы, те — у школьников третьей, а школьники третьей — у школьников первой. При этом в каждой школе отношения между классами тоже могут быть нетранзитивными — школьники из класса А чаще выигрывают у школьников из класса В, те — у школьников из класса С, а последние — у школьников из класса А (все со счетом, кратным 5:4, поскольку я работал с исходными числами из квадрата Ло Шу).
Но это не всё. Могут существовать повсеместные вложенные друг в друга нетранзитивные отношения превосходства для команд не только школ и районов, но и городов, стран, континентов, планет и их систем, галактик и т. д., и т. д. — до сколь угодно больших возможных космических образований, если бы там играли в шахматы.
Разработка строгого алгоритма рекурсивной процедуры построения (выращивания) метанетранзитивности произвольно высокого уровня из любого исходного нетранзитивного набора чисел — задача будущего исследования.
Если такой рекурсивный алгоритм возможен, то получаемые с его помощью числа, возможно, образуют фрактальную структуру при их геометрическом представлении (например, разными цветами карандашей разной длины или как-то еще). Было бы интересно изучить эти фрактальные структуры для разных изначальных нетранзитивных наборов — отличающихся количеством исходных подмножеств, количеством элементов в них и другими параметрами, — а также представить и охарактеризовать, если возможно, все эти фрактальные структуры как целое.
Александр Поддьяков, докт. психол. наук
1 Кольца Борромео. ru.wikipedia.org/wiki/Кольца_Борромео
2 Chamberland M., Herman E. A. Rock-Paper-Scissors meets Borromean rings // Math Intelligencer. 2015. V. 37(2). P. 20–25.
3 O’Keeffe M., Treacy M. M. J. Borromean rings redux. A missing link found — a Borromean triplet of Borromean triplets // Acta Crystallographica Section A: Foundations and Advances. 2023. V. 79(2). P. 217–219.
4 Поддьяков А. Н. Понимание нетранзитивности превосходства и объекты экспериментального интереса в разных областях и парадигмах. Доклад на заседании научно-теоретического семинара «Формальная философия» 30 июня 2021 года. Презентация: researchgate.net/publication/352856372;
Poddiakov A., Lebedev A. V. Intransitivity and meta-intransitivity: meta-dice, levers and other opportunities // European Journal of Mathematics. 2023. V. 9(27).
doi.org/10.1007/s40879-023-00618-z. Full text: rdcu.be/c9Aw0.
5 ru.wikipedia.org/wiki/Нетранзитивные_кости
6 Поддьяков А. Метанетранзитивные игральные кости // ТрВ-Наука. № 333 от 13 июля 2021 года.
7 Поддьяков А. Н. Пример метанетранзитивности доминирования 2-го порядка и постановка некоторых дальнейших задач. Препринт. 8 мая 2023 года;
Поддьяков А. Н. Отношения доминирования: метанетранзитивность, метатранзитивность и промежуточные комбинации отношений разных порядков. Препринт. 29 апреля 2023 года.
8 Смирнова Ю. Формула успеха: никаких формул! // Наука и жизнь. 21 августа 2012 года.
9 Гарднер М. Парадоксы комбинаторики // Гарднер М. Математические досуги. М.: Мир, 1972. С. 342–351;
Gardner M. Permutations and paradoxes in combinatorial mathematics // Scientific American. V. 209(2). P. 112–119.



 (2 оценок, среднее: 4,50 из 5)
(2 оценок, среднее: 4,50 из 5)
Пример с кольцами Борромео как раз заставляет усомниться в содержательности темы: процедура, применённая к брунновому зацеплению, даёт небрунново зацепление. Не видно ничего, никаких явлений, кроме рекурсии.
Про кольца Борромео я написал, что это лишь подводка.
Не было числовых примеров метанетранзитивности 2-го уровня (и самой постановки задачи) – теперь есть и постановка, и сконструированы примеры. Показан путь доказательства (пока не оно само), что на этой основе можно строить числовые примеры метанетранзитивности произвольно высоких уровней.
Такую возможность раньше никто не рассматривал, не думали в этом направлении. Будет ли это считаться содержательным результатом, станет ясно в том числе после журнальной публикации и появления (или непоявления) ссылок на нее.
Для сравнения можно посмотреть, что считается содержательным результатом, в научно-популярной статье:
Klarreich, E. (2023). Mathematicians roll dice and get rock-paper-scissors. Quantamagazine. January 19, 2023. https://www.quantamagazine.org/mathematicians-roll-dice-and-get-rock-paper-scissors-20230119
Не поленился, посмотрел препринт. Таблица производит впечатление, что сотни, десятки и единицы тусуются каждые сами по себе. Хотя в десятках Вы указываете на какую-то тонкость.
Вот такой как бы напрашивается подход: посмотреть, какие операции сохраняют (просто)нетранзитивность. Похоже, таких операций, в духе статьи по ссылке, много: добавление больших чисел, добавление маленьких чисел… Наверное, из-за того, что их много, и появляется возможность построить метанетранзитивность.
Вообще, судя по этой статье, сама нетранзитивность, вопреки интуиции, малосодержательна:
“Knowing that A beats B and B beats C just gives you no information about whether A beats C.”
Здесь стоит провести различение понятий “малосодержательный” и “малоинформативный” по объектам их применения.
Да, эти авторы обнаружили, что, как они подчеркивают, вопреки интуиции, данные “кость А бьет В, а В бьет С” почти не дают информации, как будут обстоять дела с битьем между А и С.
При этом утверждение о малой информативности данных “кость А бьет В, а В бьет С” для вывода об отношениях А и С информативно, содержательно.
Показ неинформативности чего-то может быть трудной задачей, а результат нести важное содержание.
Статья, в которой показана неинформативность данных “кость А бьет В, а В бьет С” для вывода об отношениях А и С получила математическую премию, а значит, часть людей считает ее очень информативной, содержательной.
Возможно, Вас также заинтересует мартовский препринт, где обосновывается важность нетранзитивности в физике (но там речь не о нетранзитивности доминирования).
Universe as a Graph (Ramsey Approach to Analysis of Physical Systems)
https://www.researchgate.net/publication/369615631
Спасибо за обращение к препринту.
Разряды чисел там тасуются сами по себе не в большей степени, чем тасуются сами по себе числа от 1 до 9 в квадрате Ло Шу.
Да, количество имеет значение – в ряде математических работ и работ по биологии с матмоделированием (например, отношений видов) показано, что чем больше наборов и чем больше элементов (объектов) в них, тем чаще там будут нетранзитивности. Нетранзитивность доминирования вообще возникает не менее, чем в трех наборах с не менее, чем тремя элементами в каждом.
За идею посмотреть, какие операции сохраняют (просто)нетранзитивность, спасибо.