Нетранзитивные позиции белых и черных в шахматах стали устойчивее, а в го им положено начало

В статье «Позиции белых и черных по принципу „камень, ножницы, бумага“» ¹ я описал цепочки шахматных позиций, в которых:

• позиция A белых предпочтительнее позиции B черных (при возможности выбора игры за белых или за черных надо выбрать позицию A белых);
• позиция B черных предпочтительнее позиции C белых;
• позиция C белых предпочтительнее позиции D черных;
• но позиция D черных предпочтительнее позиции A белых.

При этом было важно, что первый ход во всех этих позициях всегда у белых. Преподаватель шахмат Татьяна Деева пошла дальше и придумала нетранзитивные позиции с тем, что она назвала устойчивым преимуществом. Она пишет: «Попробуем сделать отношение преимущества в нетранзитивной цепочке „устойчивым“ к очереди хода: будем считать позицию одной из сторон более предпочтительной, если выигрыш достигается независимо от очереди хода, т. е. как при ходе белых, так и при ходе черных. Отношение устойчивого преимущества договоримся обозначать символом „>>“» ².

Статья подзамочная, и я приведу здесь лишь одну из сконструированных ею цепочек нетранзитивных позиций с устойчивым преимуществом.

В заключение статьи Т. Деева объясняет: «Тема нетранзитивности в шахматах относительно нова, однако ее нельзя назвать искусственно привнесенной. Элемент нетранзитивности заложен в правилах игры: в момент превращения самая слабая фигура, пешка, не сравнивается по силе с ферзем, а превосходит его. И в этюдах, и в реальных партиях встречаются ситуации, исход которых определяется именно двойственностью угрозы: возможностью превращения пешки как в ферзя, так и в коня. Таким образом, набор шахматных фигур сам по себе является нетранзитивным, а расчет материального соотношения сил на доске — гораздо более условным, чем кажется на первый взгляд. Стоит ли удивляться, что использование идеи нетранзитивности позиций способствует более глубокому пониманию шахмат?»

А как обстоят дела с возможностью нетранзитивных позиции белых и черных, например, в игре го? Я писал разным специалистам и задавал этот вопрос. В ответ путь построения таких позиций предложил Лоренц Триппель, секретарь Европейской федерации го (публикую с его разрешения, без перевода на русский, чтобы не напутать; желающие могут воспользоваться интернет-переводчиками):

“I guess the simplest way to demonstrate would be with josekis: 4 corners and each corner faces two other corners and of course it’s important in which direction they face each other, so this would be easy to prove that this kind of circular superiority will happen.

In go, in the opening it’s important to see the ladders, ladders go over the whole board and there are ladder breakers or there a no ladder breakers on the other side (ladders go like bit diagonally). This is often very important when choosing a certain joseki: if the ladder works for the opponent it’s bad (or needs another inferior? way to be played) and if it works for oneself (like killing the opponents’ stones in the ladder) it’s good.

Actually there are so many ways in how a position relates to another position that it is kind of impossible to give a value to a position in an isolated way. But still in go we call joseki only positions which are balanced in itself so the abstract concept actually exists and is very much studied. Usually it goes something like this: It’s joseki when in the other corner the opponents / own position looks like this and bad if it looks like that so it kind of already explains the relation or it says something like “if the ladder works it’s good, if it doesn’t it fails” and would not be joseki anymore”.

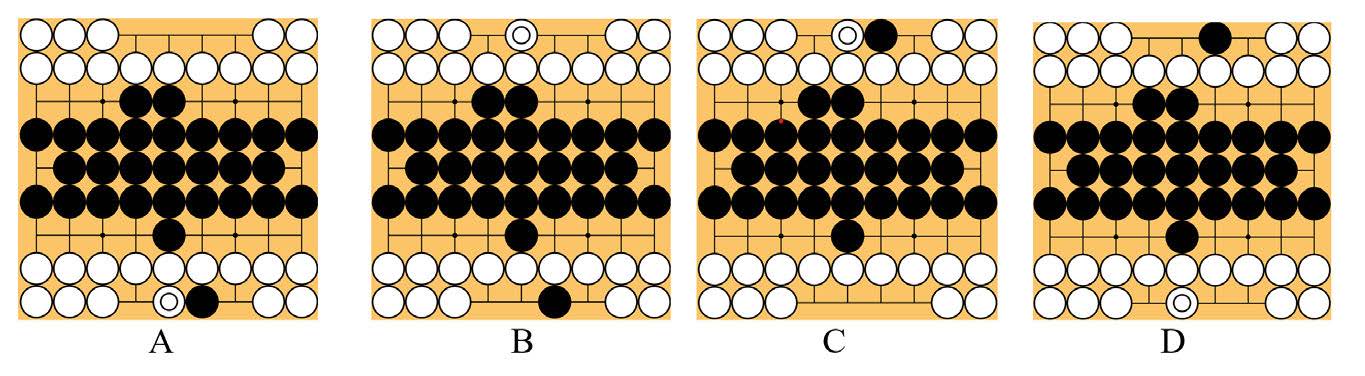
Не зная об этой переписке, Денис Федянин из Института проблем управления РАН предложил свою цепочку нетранзитивных позиций белых и черных в го ³.

Он дает следующее пояснение.

«У белых два варианта расположения камней — они отличаются только расположением белого камня — внизу (БВ) или вверху (БН). Аналогично два варианта есть у черных — черный камень вверху (ЧВ) или внизу (ЧН).

При первом ходе черных:

• в позиции A (БН, ЧН) выигрывает белый;
• в позиции B (БВ, ЧН) выигрывает черный;
• в позиции C (БВ, ЧВ) выигрывает белый;
• в позиции D (БН, ЧВ) выигрывает черный».

Итак, нетранзитивные позиции сторон сконструированы в шахматах, шашках и го. На очереди, возможно, реверси. Нетранзитивность позиций сторон оказывается общим свойства ряда достаточно сложных игр на размеченном поле, и ее наличие может быть одним из критериев этой сложности. Кроме того, на основе этой нетранзитивности можно показать, что расстояния между позициями сторон в пространстве их выигрышности не являются евклидовыми⁴ (про это — сложный текст⁵).

Александр Поддьяков, докт. психол. наук

¹ trv-science.ru/2022/11/pozicii-belyx-i-chernyx-po-principu-kamen-nozhnicy-bumaga/

² Деева Т. Оценивая преимущество: нетранзитивные позиции в шахматах // Наука и жизнь. 2023. № 4. nkj.ru/archive/articles/47905/

³ researchgate.net/publication/369370009

⁴ wiki.loginom.ru/articles/euclid-distance.html

⁵ Поддьяков А.Н. Нетранзитивные по выигрышности позиции белых и черных в шахматах // Математическая теория игр и ее приложения. 2022. № 3. С. 75-100. bit.ly/3ZNfqtm