«Задача трех тел» — разбор полета

Попробуем завести новую рубрику: «Разбор полетов НФ». Что в научной фантастике соответствует науке, что нет, почему, и как оно на самом деле. Никому не придет в голову устраивать разбор, например, «Пикника на обочине». Что такое «комариная плешь» или «ведьмин студень»? Авторы не претендуют на наукообразное объяснение и избегают ответственности, приписывая эти штуки развитой внеземной цивилизации. Никому не придет в голову критиковать и Станислава Лема за «Солярис», где он описывает прекрасным научным языком совершенно вненаучные проявления Океана — «симметриады», «асимметриады» и прочее. Но если автор использует существующие научные понятия и строит на них сюжет, приходится «отвечать за базар». Для начала разбору полетов фантазии подлежит книга Лю Цысиня «Задача трех тел» (внимание: спойлеры).

Сразу надо оговориться, что научно-фантастическая книга — не научная монография, и автор имеет право на нереалистичные допущения. Ценность книги (или ее отсутствие) совсем в другом, и мы беремся за разбор не для того, чтобы «уесть» автора, а в просветительских целях. Поскольку книгу читали (или хотя бы слышали про нее) многие, то сформировалась хорошая подготовленная почва для темы: есть цепкий информационный повод, за что спасибо автору романа.

Лю Цысинь, обложка первого издания его романа и постер китайского телесериала на ту же тему 2023 года («Википедия»)

‌

Фабула такова: в тройной звездной системе Альфа Центавра есть планета под названием Трисолярис, на которой существует цивилизация, которой всё время приходится бороться за жизнь: она то замерзает, то поджаривается, бывают стабильные периоды, которые сменяются хаосом и катаклизмами. Причина — хаотическая и непредсказуемая динамика трех тел (звезд), а непредсказуема она якобы потому, что задача трех тел не имеет аналитического решения. Над этим аналитическим решением трудится эксцентричный землянин, что составляет побочную сюжетную линию романа.

Формулировка задачи

Ньютоновская динамика трех тел описывается очень простой системой трех обыкновенных дифференциальных уравнений:

$$d^2\boldsymbol{x}_1/dt^2=GM_2(\boldsymbol{x}_2-\boldsymbol{x}_1)/{R_{12}}^3+GM_3(\boldsymbol{x}_3-\boldsymbol{x}_1)/{R_{13}}^3$$
$$d^2\boldsymbol{x}_2/dt^2=GM_1(\boldsymbol{x}_1-\boldsymbol{x}_2)/{R_{12}}^3+GM_3(\boldsymbol{x}_3-\boldsymbol{x}_2)/{R_{23}}^3$$
$$d^2\boldsymbol{x}_3/dt^2=GM_1(\boldsymbol{x}_1-\boldsymbol{x}_3)/{R_{13}}^3+GM_2(\boldsymbol{x}_2-\boldsymbol{x}_3)/{R_{23}}^3$$

Где x_i — координатный вектор i-го тела, M_i — массы тел, R_ij — расстояния между ними, G — гравитационная постоянная. Как видите, всё очень просто: каждое из тел испытывает ускорение по действием тяготения двух других. Однако, несмотря на простоту, эта система уравнений в общем случае не имеет аналитического решения, выражаемого конечной формулой. Аналитическое решение существует, но в виде бесконечного медленно сходящегося ряда. Проще решать вышеприведенные уравнения численными методами «в лоб», чем суммировать этот ряд. Простые аналитические решения задачи трех тел тоже существуют, но только для определенных конфигураций, например если тела сидят в вершинах равностороннего треугольника. Сейчас известно более тысячи конфигураций, для которых существуют периодические аналитические решения. Таких решений бесконечно много, что доказал Пуанкаре, но они составляют меру ноль, и малейшее отклонение от точных начальных условий быстро выводит систему из аналитического поведения.

Есть ли практическая необходимость в аналитическом решении? В романе Лю Цысиня таковое представляется как способ едва ли не спасения трисолярианской цивилизации, дескать, это откроет им будущее, к которому можно будет приспособиться заранее. Проблема в том, что, существуй такое решение, оно было бы неустойчивым: динамика трех тел неустойчива по существу. Ничтожная ошибка в измерении начальных условий привела бы к непредсказуемым отклонениям в скором будущем — уже через несколько динамических времен. Динамическое время в данном случае — понятие растяжимое, можно определить его как средний период обращения тел вокруг барицентра — в таком определении появляется проблема, когда одно из тел отброшено далеко, но пожертвуем строгостью ради наглядности.

Вместе с тем эволюция системы трех тел прекрасно считается численно с любой заданной точностью, в том числе и с практически бесполезной, когда ошибку определяет неточность в знании начальных условий. Поэтому усилия героя романа по аналитическому решению задачи трех тел имели бы чисто академический, а не практический интерес.

Но есть и хорошая новость: таких неудобных звездных систем, как описано в романе, т. е. долгое время находящихся в состоянии динамического хаоса, не бывает.

Какие бывают кратные звездные системы

Альфа Центавра, о которой идет речь в романе, — действительно тройная система, но совсем не такая «зловредная» — она иерархическая и стабильная. Иерархическая структура для тройной системы — это относительно тесная пара и третья звезда «на отшибе». В данном случае «на отшибе» Проксима Центавра, красный карлик — он удален на 0,2 светового года, период обращения — около 500 тыс. лет. Две другие звезды, A и B, — солнцеподобные, движутся по орбите с большой полуосью 23 астрономические единицы (расстояние больше, чем от Солнца до Урана, и меньше, чем до Нептуна) с периодом около 80 лет. У каждой звезды возможны планеты на стабильных орбитах. У Проксимы точно есть одна и, вероятно, еще две. У звезды A есть неподтвержденная планета-гигант (или субгигант типа Нептуна) на орбите, близкой к земной. Это еще один уровень иерархии — такая орбита стабильна. Если у той планеты есть крупный спутник — на нем возможна жизнь, поскольку орбита лежит в зоне обитаемости. Это будет уже четвертый уровень иерархии. Все уровни стабильны, важно, чтобы между ними была большая разница в масштабах — примерно на порядок.

Рис. 1. Система Альфа Центавра. На снимке слева яркая звезда — пара А и B. Проксима Центавра — красноватая точка в центре красного кружка (Skatebiker / «Википедия»). Сверху — снимок космического телескопа «Хаббл» пары A и B (ESA/NASA)

‌

Подавляющее большинство звездных систем именно иерархические. Исключения есть, но это молодые системы с большими динамическими временами — они еще не релаксировали. Итак, среди кратных звезд не существует систем, долгое время находящихся в состоянии динамического хаоса, как это описано в «Задаче трех тел». Но если мы возьмем три тела с примерно одинаковыми массами на примерно одинаковых расстояниях друг от друга и запустим их в произвольных направлениях — так, чтобы они были гравитационно связаны, — то с большой вероятность получится именно система с хаотической динамикой. Звезды рождаются группами именно таким образом. Почему же мы не наблюдаем подобных систем?

Игра «третий лишний»

Причина проста: в хаотической системе с наибольшей вероятностью одно из тел выкидывается из гравитационно связанной системы обычно за пару десятков динамических времен или даже раньше. Либо система небольшого числа тел становится иерархической сразу, либо она, пройдя через стадию хаоса, выкидывает все лишние тела, пока не станет устойчивой — либо двойной, либо иерархической. Это, так сказать, проза жизни: распад системы — самый распространенный финал.

С одной стороны, численное моделирование системы трех тел — довольно простая и весьма распространенная забава. Существуют простые общедоступные компьютерные программы: задаешь начальные условия системы и смотришь, как движутся частицы, что с ними происходит. Проблема в том, что начальные условия — точка в 18-мерном фазовом пространстве: ни визуализировать, ни разобраться — есть ли там какие-то закономерности в судьбе системы в зависимости от начальных условий. И это при фиксированном соотношении масс!

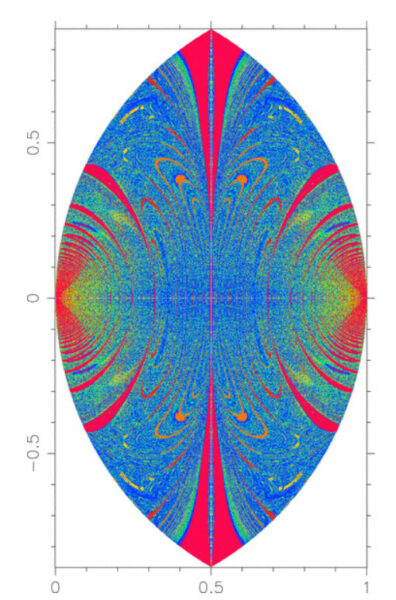
Поэтому, чтобы увидеть хоть какие-нибудь закономерности, надо брать какое-то двумерное подмножество начальных параметров — лишь так можно составить какое-то впечатление о характере задачи. Есть, например, «гомологическая карта» Агекяна — Аносовой: берем три неподвижных тела равной массы, помещаем одно тело в начало координат (0; 0), второе — в точку (1; 0), третье — в точку (x, y); отпускаем их и прослеживаем эволюцию системы на компьютере. В этой конкретной игре единица времени берется равной 1/2π от начального орбитального периода легкого пробного тела вокруг тела 1 на расстоянии 1. На рис. 2 показан результат моделирования из статьи [1].

Цвет показывает время до распада — когда одно из тел выходит на траекторию вылета из системы.

Цветовая шкала здесь расширена: темно-синий обозначает время жизни дольше 20 динамических времен.

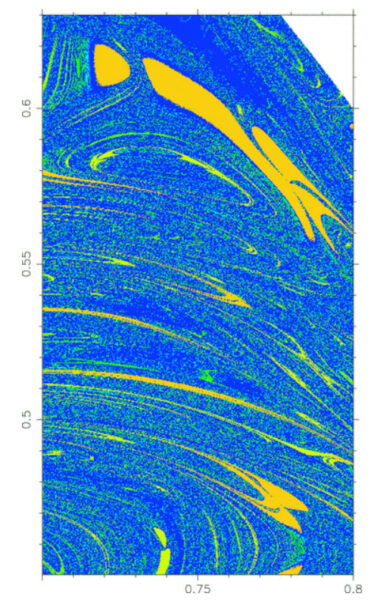
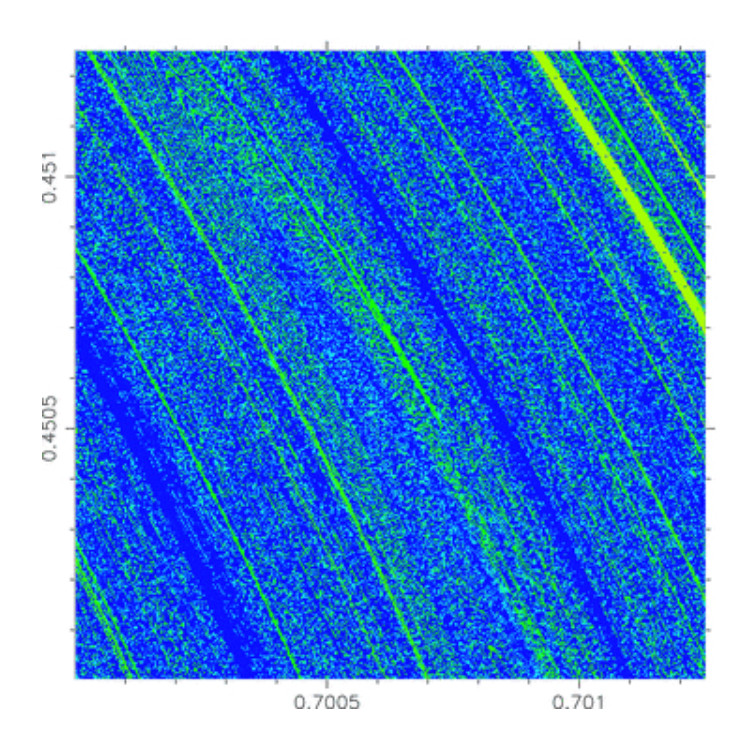
С первого взгляда картинка выглядит красивой и упорядоченной — красные дуги (быстрый распад), дуги других цветов — более медленный распад. На увеличенном фрагменте карты картина представляется более сложной — есть области стабильного распада, но большая часть — пестрая: стоит немного сдвинуть начальные условия — и время жизни системы резко меняется. А на рис. 4 показан вообще «микроскопический» кусок карты, и по-прежнему картина пестрая. Такое поведение системы принято называть «фрактальным». Авторы статьи утверждают, что фрактальное поведение покрывает 71,4% площади карты, причем это настоящий фрактал с определенной фрактальной (хаусдорфовской) размерностью D = 1,5. Эта же карта исследована до гораздо больших времен в работе [2]. Там найдены точки, где система живет более тысячи динамических времен. Подобные точки близки к стабильным периодическим решениям меры ноль, но близкие долгоживущие решения имеют уже конечный фазовый объем в начальных условиях. При этом периодические решения бывают очень интересными, например осциллирующими, — они радикально меняют свое поведение, потом возвращаются к прежней картине и так до бесконечности. Видимо, что-то подобное имел в виду автор «Задачи трех тел», описывая мир, где периоды хаоса чередуются с периодами стабильности. У таких осциллирующих решений тоже мера ноль, но, может быть, есть системы очень близкие к ним? К сожалению, в реальной жизни есть еще внешние возмущения от пролетающих мимо звезд, которые разрушают конфигурации, близкие с стабильным периодическим решениям. К ничтожно малому стартовому объему добавляются «непредусмотренные» возмущения. Возможно, хаотическая система может держаться в своем хаосе сотни тысяч, может быть, даже миллион лет, но за сотни миллионов, требуемых для возникновения жизни, точно либо распадется до бинарной, либо превратится в иерархическую. Вот мы и не видим таких систем, за исключением молодых с большим динамическим временем.

Кстати, авторы упомянутых статей обращают на фактическую необратимость динамики трех тел во времени. Отклонения траекторий при бесконечно малом отклонении начальных условий со временем нарастают экспоненциально. Формально каждое решение обратимо во времени, фактически же оно необратимо в присутствии сколь угодно малых возмущений. То есть уже на этом уровне возникает стрела времени.

Что можно отнести к научной фантастике

Здесь применимо нечто вроде критерия Поппера. Попробуем сформулировать его так: «если фантастическое допущение автора может быть опровергнуто строго научными аргументами, то оно принадлежит к жанру научной фантастики». Причем чем больше усилий требуется, чтобы опровергнуть допущение, тем научней фантастика. «Ведьмин студень» Стругацких опровержению не подлежит, поскольку авторы и не пытались растолковать, что это такое в рамках науки. Поэтому «Пикник на обочине» не относится к строго научной фантастике, отчего он не становится хуже. А тут мы чисто научными аргументами опровергли концепцию Трисоляриса из «Задачи трех тел», при этом нам пришлось закапываться довольно глубоко и прибегать к просветительски значимому анализу. То есть эта часть романа по праву может быть названа научно-фантастической. Мы могли бы ограничиться тем, чтобы сказать: «Реальная Альфа Центавра — совсем другая система», — но это было бы неинтересно и не познавательно.

Касательно других фантастических допущений романа. Радиолокация Солнца и усиление радиосигнала его недрами. Здесь наиболее интересно утверждение о фазовом разделе внутри Солнца — резкая граница с падением энергии рентгеновских фотонов и, видимо, уровня ионизации, например железа (об этом автор не пишет, но я бы добавил именно эту деталь). Я даже сходу не могу ее опровергнуть. Скорее всего, ерунда, но это надо считать. Таким образом, данное допущение вполне в рамках научной фантастики. Тем более, что подобные фазовые границы встречаются в межзвездной среде — зоны НI и НII. А то, что радиоволны проникают до этой границы и усиливаются на ней, — ерунда очевидная, это всё еще научная фантастика, поскольку контраргумент — длина поглощения радиоволн в плазме. Правда, этот случай уже ближе к фэнтези или космоопере. А вот история про два «умных» протона, запущенных от Трисоляриса к Земле,— это чистые словеса, там не за что зацепиться. Нагромождение антуражных словес, которые можно было бы передать эквивалентной фразой: «Жители Трисоляриса заколдовали два протона и запустили их к Земле, чтобы те навели на земных ученых порчу». Это совершенно вне рамок научной фантастики.

Таким образом, роман «Задача трех тел» можно отнести к гибридным. Еще раз подчеркну, что это ничего не говорит о его качестве. А есть ли чисто научно-фантастические книги и фильмы? Да сколько угодно, хотя их доля среди того, что именуется научной фантастикой невелика. Из относительно недавнего — «Интерстеллар» (некоторые пассажи опровергаются легко, некоторые требуют усилий), «Марсианин» Энди Вейера, «Ложная слепота» Питера Уотса, книги Грега Игана (многие допущения вполне научны — не только фальсифицируемы, но и верифицируемы). Из тех книг, где фантастические допущения попросту правильны и годятся в качестве приложения к учебнику физики, можно привести «Экспедицию „Тяготение“» Хола Клемента. Конечно, этот анализ не претендует на полноту. Надеюсь, продолжение последует.

Борис Штерн

1. Lehto H. J., Kotiranta S., Valtonen M. J., Heinämäki P., Mikkola S., Chernin A. D. Mapping the three-body system – decay time and reversibility // Monthly Notices of the Royal Astronomical Society, Volume 388, Issue 3, 11. August 2008. P. 965–970. doi.org/10.1111/j.1365-2966.2008.13450.x

2. Boekholt T. C. N., Portegies Zwart S. F., Valtonen M. Gargantuan chaotic gravitational three-body systems and their irreversibility to the Planck length // Monthly Notices of the Royal Astronomical Society, 10, 2. April 2020. DOI: 10.1093/mnras/staa452